No CrossRef data available.
Article contents
A theorem on a finite difference operator and its connection with the Poisson distribution
Published online by Cambridge University Press: 09 April 2009
Extract
The well-known Taylor expansion of a function around a point a can be formally written as 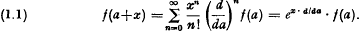 The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. We shall study the situation when the differential operator d/da is replaced by the finite difference operator Δh/h, where the operator Δh, is defined by
The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. We shall study the situation when the differential operator d/da is replaced by the finite difference operator Δh/h, where the operator Δh, is defined by 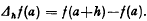 In general,
In general, 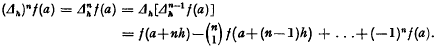 Then we have the following theorem.
Then we have the following theorem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1966


