Tables of the logaritm of iteration of e^x—1

Extract

In the preceding paper ¹) one of us has proposed a definition for the “best” or most regularly growing fractional iterates of logarithmico-exponential type functions. The definition was essentially based on two observations. First, that the functional equation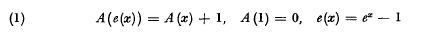 has exactly one solution with the property that is totally monotonic for every x > 0. Secondly, that if f(x) is a logarithmicoexponential function such that then the Abel equation has (apart from the arbitrariness of an additive constant) exactly one solution with the property that exists) and the same is true for any reasonably well-behaved function with property (3) whose manner of growth does not transcend Hardy's scale of L-functions. Thus every such function has a uniquely determined family of fractional iterates given by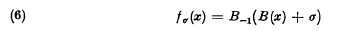 and these fσ(x) may be regarded as the most regularly growing iterates of f(x).