Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T20:03:09.543Z Has data issue: false hasContentIssue false
  • English
  • Français

SURVEY: SIXTY YEARS OF DOUGLAS–RACHFORD

Part of: Existence theories Miscellaneous applications of functional analysis Calculus of variations and optimal control; optimization

Published online by Cambridge University Press:  20 February 2020

SCOTT B. LINDSTROM Open the ORCID record for SCOTT B. LINDSTROM [Opens in a new window]  and
BRAILEY SIMS
SCOTT B. LINDSTROM*
Affiliation:
CARMA, University of Newcastle, Australia
BRAILEY SIMS
Affiliation:
CARMA, University of Newcastle, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Douglas–Rachford method is a splitting method frequently employed for finding zeros of sums of maximally monotone operators. When the operators in question are normal cone operators, the iterated process may be used to solve feasibility problems of the following form: Find 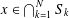$x\in \bigcap _{k=1}^{N}S_{k}$. The success of the method in the context of closed, convex, nonempty sets $S_{1},\ldots ,S_{N}$ is well known and understood from a theoretical standpoint. However, its performance in the nonconvex context is less well understood, yet it is surprisingly impressive. This was particularly compelling to Jonathan M. Borwein who, intrigued by Elser, Rankenburg and Thibault’s success in applying the method to solving sudoku puzzles, began an investigation of his own. We survey the current body of literature on the subject, and we summarize its history. We especially commemorate Professor Borwein’s celebrated contributions to the area.

Keywords

Douglas–Rachfordfeasibilityprojection algorithmsiterative methodsdiscrete dynamical systems

MSC classification

Primary: 46N10: Applications in optimization, convex analysis, mathematical programming, economics 49J53: Set-valued and variational analysis 49-02: Research exposition (monographs, survey articles)
Secondary: 49-03: Historical (must also be assigned at least one classification number from Section 01)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 3 , June 2021 , pp. 333 - 370
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by G. Willis

This work is dedicated to the memory of Jonathan M. Borwein our greatly missed friend, mentor and colleague. His influence on both the topic at hand, as well as his impact on the present authors personally, cannot be overstated.

References

Alwadani, S., Bauschke, H. H., Moursi, W. M. and Wang, X., ‘On the asymptotic behaviour of the Aragón Artacho–Campoy algorithm’, Oper. Res. Let. 46(6) (2018), 585–587.Google Scholar
Artacho, F. J. A. and Borwein, J. M., ‘Global convergence of a non-convex Douglas–Rachford iteration’, J. Global Optim. 57(3) (2013), 753–769.Google Scholar
Artacho, F. J. A., Borwein, J. M. and Tam, M. K., ‘Recent results on Douglas–Rachford methods’, Serdica Math. J. 39 (2013), 313–330.Google Scholar
Artacho, F. J. A., Borwein, J. M. and Tam, M. K., ‘Douglas–Rachford feasibility methods for matrix completion problems’, ANZIAM J. 55(4) (2014), 299–326.Google Scholar
Artacho, F. J. A., Borwein, J. M. and Tam, M. K., ‘Recent results on Douglas–Rachford methods for combinatorial optimization problems’, J. Optim. Theory Appl. 163(1) (2014), 1–30.Google Scholar
Artacho, F. J. A., Borwein, J. M. and Tam, M. K., ‘Global behavior of the Douglas–Rachford method for a nonconvex feasibility problem’, J. Global Optim. 65(2) (2016), 309–327.Google Scholar
Artacho, F. J. A and Campoy, R., ‘Solving graph coloring problems with the Douglas–Rachford algorithm’, Set-Valued Var. Anal. 26(2) (2018), 277–304.Google Scholar
Artacho, F. J. A. and Campoy, R., ‘Computing the resolvent of the sum of maximally monotone operators with the averaged alternating modified reflections algorithm’, J. Optim. Theory Appl. 181(3) (2019), 709–726.Google Scholar
Artacho, F. J. A. and Campoy, R., ‘A new projection method for finding the closest point in the intersection of convex sets’, Comput. Optim. Appl. 69(1) (2018), 99–132.Google Scholar
Artacho, F. J. A., Campoy, R., Kotsireas, I. and Tam, M. K., ‘A feasibility approach for constructing combinatorial designs of circulant type’, J. Combin. Optim. 35(4) (2018), 1061–1085.Google Scholar
Artacho, F. J. A., Censor, Y. and Gibali, A., ‘The cyclic Douglas–Rachford algorithm with r-sets-Douglas–Rachford operators’, Optim. Methods Softw. 34(4) (2019), 875–889.Google Scholar
Arrow, K., Hurwicz, L. and Uzawa, H., ‘Studies in nonlinear programming’, (Cambridge University Press, 1958).Google Scholar
Artacho, F. J., Campoy, R. and Elser, V., ‘An enhanced formulation for solving graph coloring problems with the Douglas–Rachford algorithm’, Preprint, (2018), arXiv:1808.01022.Google Scholar
Attouch, H., ‘On the maximality of the sum of two maximal monotone operators’, Technical report, Wisconsin University, Madison Mathematics Research Center, (1979).Google Scholar
Bansal, P., ‘Code for solving Tetravex using Douglas–Rachford algorithm’, (2010), available at https://people.ok.ubc.ca/bauschke/Pulkit/pulkitreport.pdf.Google Scholar
Bauschke, H. H., Cruz, J. Y. B., Nghia, T. T. A., Phan, H. M. and Wang, X., ‘The rate of linear convergence of the Douglas–Rachford algorithm for subspaces is the cosine of the Friedrichs angle’, J. Approx. Theory 185 (2014), 63–79.Google Scholar
Bauschke, H. H. and Borwein, J. M., ‘On projection algorithms for solving convex feasibility problems’, SIAM Rev. 38(3) (1996), 367–426.Google Scholar
Bauschke, H. H., Boţ, R. I., Hare, W. L. and Moursi, W. M., ‘Attouch–Théra duality revisited: paramonotonicity and operator splitting’, J. Approx. Theory 164(8) (2012), 1065–1084.Google Scholar
Bauschke, H. H., Burke, J., Deutsch, F., Hundal, H. and Vanderwerff, J., ‘A new proximal point iteration that converges weakly but not in norm’, Proc. Amer. Math. Soc. 133(6) (2005), 1829–1835.Google Scholar
Bauschke, H. H. and Combettes, P. L., Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 1st edn, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC (Springer, Cham, 2011).Google Scholar
Bauschke, H. H., Combettes, P. L. and Luke, D. R., ‘Phase retrieval, error reduction algorithm, and Fienup variants: a view from convex optimization’, J. Opt. Soc. Amer. A 19(7) (2002), 1334–1345.Google Scholar
Bauschke, H. H., Combettes, P. L. and Luke, D. R., ‘Hybrid projection–reflection method for phase retrieval’, JOSA A 20(6) (2003), 1025–1034.Google Scholar
Bauschke, H. H., Combettes, P. L. and Luke, D. R., ‘Finding best approximation pairs relative to two closed convex sets in Hilbert spaces’, J. Approx. Theory 127(2) (2004), 178–192.Google Scholar
Bauschke, H. H., Cruz, J. Y. B., Nghia, T. T. A., Pha, H. M. and Wang, X., ‘Optimal rates of linear convergence of relaxed alternating projections and generalized Douglas–Rachford methods for two subspaces’, Numer. Algorithms 73(1) (2016), 33–76.Google Scholar
Bauschke, H. H. and Dao, M. N., ‘On the finite convergence of the Douglas–Rachford algorithm for solving (not necessarily convex) feasibility problems in Euclidean spaces’, SIAM J. Optim. 27(1) (2017), 507–537.Google Scholar
Bauschke, H. H., Dao, M. N. and Lindstrom, S. B., ‘The Douglas–Rachford algorithm for a hyperplane and a doubleton’, J. Glob. Optim. 74(1) (2019), 79–93.Google Scholar
Bauschke, H. H., Dao, M. N. and Moursi, W. M., ‘On Fejér monotone sequences and nonexpansive mappings’, Preprint, (2015), arXiv:1507.05585.Google Scholar
Bauschke, H. H., Dao, M. N. and Moursi, W. M., ‘The Douglas–Rachford algorithm in the affine-convex case’, Oper. Res. Lett. 44(3) (2016), 379–382.Google Scholar
Bauschke, H. H., Dao, M. N., Noll, D. and Phan, H. M., ‘On Slaters condition and finite convergence of the Douglas–Rachford algorithm for solving convex feasibility problems in Euclidean spaces’, J. Global Optim. 65(2) (2016), 329–349.Google Scholar
Bauschke, H. H., Dao, M. N., Noll, D. and Phan, H. M., ‘Proximal point algorithm, Douglas–Rachford algorithm and alternating projections: a case study’, J. Convex Anal. 23(1) (2016), 237–261.Google Scholar
Bauschke, H. H., Hare, W. L. and Moursi, W. M., ‘Generalized solutions for the sum of two maximally monotone operators’, SIAM J. Control Optim. 52(2) (2014), 1034–1047.Google Scholar
Bauschke, H. H., Hare, W. L. and Moursi, W. M., ‘On the range of the Douglas–Rachford operator’, Math. Oper. Res. 41(3) (2016), 884–897.Google Scholar
Bauschke, H. H., Koch, V. R. and Phan, H. M., ‘Stadium norm and Douglas–Rachford splitting: a new approach to road design optimization’, Oper. Res. 64(1) (2015), 201–218.Google Scholar
Bauschke, H. H., Lukens, B. and Moursi, W. M., ‘Affine nonexpansive operators, Attouch–Théra duality and the Douglas–Rachford algorithm’, Set-Valued Var. Anal. 25(3) (2017), 481–505.Google Scholar
Bauschke, H. H. and Moursi, W. M., ‘The Douglas–Rachford algorithm for two (not necessarily intersecting) affine subspaces’, SIAM J. Optim. 26(2) (2016), 968–985.Google Scholar
Bauschke, H. H. and Moursi, W. M., ‘On the order of the operators in the Douglas–Rachford algorithm’, Opt. Lett. 10(3) (2016), 447–455.Google Scholar
Bauschke, H. H. and Moursi, W. M., ‘On the Douglas–Rachford algorithm’, Math. Program. 164(1-2) (2017), 263–284.Google Scholar
Bauschke, H. H. and Noll, D., ‘On the local convergence of the Douglas–Rachford algorithm’, Arch. Math. (Basel) 102(6) (2014), 589–600.Google Scholar
Bauschke, H. H., Noll, D. and Phan, H. M., ‘Linear and strong convergence of algorithms involving averaged nonexpansive operators’, J. Math. Anal. Appl. 421(1) (2015), 1–20.Google Scholar
Bauschke, H. H., Schaad, J. and Wang, X., ‘On Douglas–Rachford operators that fail to be proximal mappings’, Math. Program. 168(1-2) (2018), 55–61.Google Scholar
Behling, R., Bello-Cruz, J. Y. and Santos, L.-R., ‘On the linear convergence of the circumcentered-reflection method’, Oper. Res. Lett. 46(2) (2018), 159–162.Google Scholar
Behling, R., Bello-Cruz, J. Y. and Santos, L.-R., ‘Circumcentering the Douglas–Rachford method’, Numer. Algorithms 78 (2018), 759–776.Google Scholar
Benoist, J., ‘The Douglas–Rachford algorithm for the case of the sphere and the line’, J. Glob. Optim. 63 (2015), 363–380.Google Scholar
Bertsekas, D. P., Convex Optimization Algorithms (Athena Scientific, Belmont, MA, 2015).Google Scholar
Borwein, J. M. and Giladi, O., ‘Ergodic behaviour of a Douglas–Rachford operator away from the origin’, Preprint, (2017), arXiv:1708.09068.Google Scholar
Borwein, J. M. and Lewis, A. S., Convex Analysis and Nonlinear Optimization: Theory and Examples, 2nd edition (Springer, New York, 2006).Google Scholar
Borwein, J. M., Li, G. and Tam, M. K., ‘Convergence rate analysis for averaged fixed point iterations in common fixed point problems’, SIAM J. Optim. 27(1) (2017), 1–33.Google Scholar
Borwein, J. M., Lindstrom, S. B., Sims, B., Skerritt, M. and Schneider, A., ‘Dynamics of the Douglas–Rachford method for ellipses and p-spheres’, Set-Valued Anal. 26(2) (2018), 385–403.Google Scholar
Borwein, J. M. and Sims, B., ‘The Douglas–Rachford algorithm in the absence of convexity’, in: Fixed Point Algorithms for Inverse Problems in Science and Engineering, Springer Optimization and Its Applications, 49 (eds. Bauschke, H. H., Burachik, R. S., Combettes, P. L., Elser, V., Luke, D. R. and Wolkowicz, H.) (Springer, Science and Business Media, 2011), 93–109.Google Scholar
Borwein, J. M., Sims, B. and Tam, M. K., ‘Norm convergence of realistic projection and reflection methods’, Optimization 64(1) (2015), 161–178.Google Scholar
Borwein, J. M. and Tam, M. K., ‘Reflection methods for inverse problems with applications to protein conformation determination’, in: Springer Volume on the CIMPA School Generalized Nash Equilibrium Problems, Bilevel Programming and MPEC, New Delhi, India (Springer, Singapore, 2017), 83–100.Google Scholar
Borwein, J. M. and Tam, M. K., ‘A cyclic Douglas–Rachford iteration scheme’, J. Optim. Theory Appl. 160 (2014), 1–29.Google Scholar
Boţ, R. I., Csetnek, E. R. and Hendrich, C., ‘Inertial Douglas–Rachford splitting for monotone inclusion problems’, Appl. Math. Comput. 256 (2015), 472–487.Google Scholar
Boţ, R. I. and Hendrich, C., ‘A Douglas–Rachford type primal-dual method for solving inclusions with mixtures of composite and parallel-sum type monotone operators’, SIAM J. Optim. 23(4) (2013), 2541–2565.Google Scholar
Bregman, L. M., ‘The method of successive projection for finding a common point of convex sets’, Sov. Math. Dok. 162(3) (1965), 688–692.Google Scholar
Brezis, H., Operateurs Maximaux Monotones et Semi-Groupes de Contractions dans les Espaces de Hilbert, North-Holland Mathematics Studies, 5 (Elsevier, 1973).Google Scholar
Brian, P. L. T., ‘A finite-difference method of high-order accuracy for the solution of three-dimensional transient heat conduction problems’, AIChE J. 7(3) (1961), 367–370.Google Scholar
Briceño-Arias, L. M., ‘Forward-Douglas–Rachford splitting and forward-partial inverse method for solving monotone inclusions’, Optimization 64(5) (2015), 1239–1261.Google Scholar
Cegielski, A., Iterative Methods for Fixed Point Problems in Hilbert Spaces, Lecture Notes in Mathematics, 2057 (Springer, Heidelberg, 2012).Google Scholar
Censor, Y. and Mansour, R., ‘New Douglas–Rachford algorithmic structures and their convergence analyses’, SIAM J. Optim. 26(1) (2016), 474–487.Google Scholar
Chan, T. F. C. and Glowinski, R., Finite Element Approximation and Iterative Solution of a Class of Mildly Non-Linear Elliptic Equations (Computer Science Department, Stanford University, Stanford, 1978).Google Scholar
Cinderella (software). Available at https://cinderella.de/tiki-index.php, (2016).Google Scholar
Combettes, P. L., ‘Solving monotone inclusions via compositions of nonexpansive averaged operators’, Optimization 53(5-6) (2004), 475–504.Google Scholar
Combettes, P. L. and Pesquet, J.-C., ‘A Douglas–Rachford splitting approach to nonsmooth convex variational signal recovery’, IEEE J. Sel. Top. Signal Process. 1(4) (2007), 564–574.Google Scholar
Combettes, P. L. and Pesquet, J.-C., ‘Proximal splitting methods in signal processing’, in: Fixed-Point Algorithms for Inverse Problems in Science and Engineering (Springer, New York, 2011), 185–212.Google Scholar
Combettes, P. L. and Pesquet, J.-C., ‘Stochastic quasi-Fejér block-coordinate fixed point iterations with random sweeping’, SIAM J. Optim. 25(2) (2015), 1221–1248.Google Scholar
Dao, M. N. and Phan, H. M., ‘Linear convergence of projection algorithms’, Math. Oper. Res. 44(2) (2019), 715–738.Google Scholar
Dao, M. N. and Phan, H. M., ‘Adaptive Douglas–Rachford splitting algorithm for the sum of two operators’, SIAM J. Optim. 29(4) (2019), 2697–2724.Google Scholar
Dao, M. N. and Tam, Matthew .K., ‘A Lyapunov-type approach to convergence of the Douglas–Rachford algorithm’, J. Global Optim. 73(1) (2019), 83–112.Google Scholar
Davis, D. and Yin, W., ‘Convergence rate analysis of several splitting schemes’, in: Splitting Methods in Communication, Imaging, Science, and Engineering (Springer, Cham, 2016), 115–163.Google Scholar
Pierro, A. R. D., ‘From parallel to sequential projection methods and vice versa in convex feasibility: results and conjectures’, in: Inherently Parallel Algorithms in Feasibility and Optimization and their Applications (Haifa, 2000), Studies in Computational Mathematics, 8 (North-Holland, Amsterdam, 2001), 187–201.Google Scholar
Demanet, L. and Zhang, X., ‘Eventual linear convergence of the Douglas–Rachford iteration for basis pursuit’, Math. Comput. 85(297) (2016), 209–238.Google Scholar
Millán, R. Díaz, Lindstrom, Scott B. and Roshchina, Vera, ‘Comparing averaged relaxed cutters and projection methods: theory and examples’, From Analysis to Visualization: A Celebration of the Life and Legacy of Jonathan M. Borwein, Callaghan, Australia, September 2017, Springer Proceedings in Mathematics and Statistics (2020), to appear.Google Scholar
Douglas, J. Jr. and Rachford, H. H. Jr, ‘On the numerical solution of heat conduction problems in two and three space variables’, Trans. Amer. Math. Soc. 82 (1956), 421–439.Google Scholar
Drusvyatskiy, D., Ioffe, A. D. and Lewis, A. S., ‘Alternating projections and coupling slope’, Preprint, (2014), arXiv:1401.7569, 1–17.Google Scholar
Eckstein, J., ‘Splitting methods for monotone operators with applications to parallel optimization’, PhD Thesis, Massachusetts Institute of Technology, (1989).Google Scholar
Eckstein, J. and Bertsekas, D. P., ‘On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators’, Math. Prog. 55(3) (1992), 293–318.Google Scholar
Eckstein, J. and Svaiter, B. F., ‘A family of projective splitting methods for the sum of two maximal monotone operators’, Math. Program. 111(1-2) (2008), 173–199.Google Scholar
Eckstein, J. and Svaiter, B. F., ‘General projective splitting methods for sums of maximal monotone operators’, SIAM J. Control Optim. 48(2) (2009), 787–811.Google Scholar
Eckstein, J. and Yao, W., ‘Understanding the convergence of the alternating direction method of multipliers: theoretical and computational perspectives’, Pacific J. Optim. 11(4) (2015), 619–644.Google Scholar
Elser, V., Private communication.Google Scholar
Elser, V., ‘Phase retrieval by iterated projections’, JOSA A 20(1) (2003), 40–55.Google Scholar
Elser, V., ‘Matrix product constraints by projection methods’, J. Global Optim. 68(2) (2017), 329–355.Google Scholar
Elser, V., ‘The complexity of bit retrieval’, IEEE Trans. Inform. Theory 64(1) (2018), 412–428.Google Scholar
Elser, V., Lan, T.-Y. and Bendory, T., ‘Benchmark problems for phase retrieval’, SIAM J. Imag. Sci. 11(4) (2018), 2429–2455.Google Scholar
Elser, V., Rankenburg, I. and Thibault, P., ‘Searching with iterated maps’, Proc. Natl. Acad. Sci. USA 104(2) (2007), 418–423.Google Scholar
Fält, M. and Giselsson, P., ‘Optimal convergence rates for generalized alternating projections’, in: 2017 IEEE 56th Annual Conference on Decision and Control (CDC) (IEEE, 2017), 2268–2274.Google Scholar
Fienup, J. R., ‘Phase retrieval algorithms: a comparison’, Appl. Opt. 21(15) (1982), 2758–2769.Google Scholar
Fortin, M. and Glowinski, R., Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems, Vol. 15 (Elsevier, 2000).Google Scholar
Franklin, D. J., Private communication.Google Scholar
Franklin, D. J., ‘Projection algorithms for non-separable wavelets and Clifford Fourier analysis’, PhD Thesis, University of Newcastle, (2018).Google Scholar
Fukushima, M., ‘A relaxed projection method for variational inequalities’, Math. Program. 35(1) (1986), 58–70.Google Scholar
Fukushima, M., ‘The primal Douglas–Rachford splitting algorithm for a class of monotone mappings with application to the traffic equilibrium problem’, Math. Program. 72(1) (1996), 1–15.Google Scholar
Gabay, D., ‘Applications of the method of multipliers to variational inequalities’, in: Studies in Mathematics and its Applications, Vol. 15, Ch. ix (Elsevier, 1983), 299–331.Google Scholar
Gabay, D. and Mercier, B., ‘A dual algorithm for the solution of nonlinear variational problems via finite element approximation’, Comput. Math. Appl. 2(1) (1976), 17–40.Google Scholar
Giselsson, P., ‘Tight global linear convergence rate bounds for Douglas–Rachford splitting’, J. Fixed Point Theory Appl. 19(4) (2017), 2241–2270.Google Scholar
Giselsson, P. and Boyd, S., ‘Diagonal scaling in Douglas–Rachford splitting and ADMM’, in: 53rd IEEE Conference on Decision and Control, Los Angeles, CA, 15–17 December, 2014 (IEEE, 2014), 5033–5039.Google Scholar
Giselsson, P. and Boyd, S., ‘Linear convergence and metric selection for Douglas–Rachford splitting and ADMM’, IEEE Trans. Automat. Control 62(2) (2017), 532–544.Google Scholar
Glowinski, R., ‘On alternating direction methods of multipliers: a historical perspective’, in: Modeling, Simulation and Optimization for Science and Technology (Springer, Dordrecht, 2014), 59–82.Google Scholar
Glowinski, R. and Marroco, A., ‘Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires’, Revue française d’automatique, informatique, recherche opérationnelle. Analyse numérique 9(R2) (1975), 41–76.Google Scholar
Glowinski, R., Osher, S. J. and Yin, W., Splitting Methods in Communication, Imaging, Science, and Engineering (Springer, 2017).Google Scholar
Goldstein, T. and Osher, S., ‘The split Bregman method for L1-regularized problems’, SIAM J. Imag. Sci. 2(2) (2009), 323–343.Google Scholar
Gravel, S. and Elser, V., ‘Divide and concur: a general approach to constraint satisfaction’, Phys. Rev. E 78(3) (2008), 036706.Google Scholar
Grussler, C. and Giselsson, P., ‘Local convergence of proximal splitting methods for rank constrained problems’, in: 56th IEEE Conference on Decision and Control, Melboune, 12–15 December, 2017 (IEEE, 2017), 702–708.Google Scholar
He, B. and Yuan, X., ‘On the O(1/n) convergence rate of the Douglas–Rachford alternating direction method’, SIAM J. Numer. Anal. 50(2) (2012), 700–709.Google Scholar
He, B. and Yuan, X., ‘On non-ergodic convergence rate of Douglas–Rachford alternating direction method of multipliers’, Numer. Math. 130(3) (2015), 567–577.Google Scholar
He, B. and Yuan, X., ‘On the convergence rate of Douglas–Rachford operator splitting method’, Math. Program. 153(2) (2015), 715–722.Google Scholar
Hesse, R. and Luke, D. R., ‘Nonconvex notions of regularity and convergence of fundamental algorithms for feasibility problems’, SIAM J. Optim. 23(4) (2013), 2397–2419.Google Scholar
Hesse, R., Luke, D. R. and Neumann, P., ‘Alternating projections and Douglas–Rachford for sparse affine feasibility’, IEEE Trans. Signal Process. 62(18) (2014), 4868–4881.Google Scholar
Hundal, H. S., ‘An alternating projection that does not converge in norm’, Nonlinear Anal.: Theory Methods Appl. 57(1) (2004), 35–61.Google Scholar
Kruger, A. Y., ‘About regularity of collections of sets’, Set-Valued Anal. 14(2) (2006), 187–206.Google Scholar
Kruger, A. Y., ‘About intrinsic transversality of pairs of sets’, Set-Valued Var. Anal. 26(1) (2018), 111–142.Google Scholar
Lamichhane, B. P., Lindstrom, S. B. and Sims, B., ‘Application of projection algorithms to differential equations: boundary value problems’, ANZIAM J. 61(1) (2019), 23–46.Google Scholar
Lewis, A. S., Luke, D. R. and Malick, J., ‘Local linear convergence for alternating and averaged nonconvex projections’, Found. Comput. Math. 9(4) (2009), 485–513.Google Scholar
Li, G. and Pong, T. K., ‘Douglas–Rachford splitting for nonconvex optimization with application to nonconvex feasibility problems’, Math. Program. 159(1-2, Ser. A) (2016), 371–401.Google Scholar
Lindstrom, S. B., Sims, B. and Skerritt, M. P., ‘Computing intersections of implicitly specified plane curves’, Nonlinear Convex. Anal. 18(3) (2017), 347–359.Google Scholar
Lions, P.-L. and Mercier, B., ‘Splitting algorithms for the sum of two nonlinear operators’, SIAM J. Numer. Anal. 16(6) (1979), 964–979.Google Scholar
Luke, D. R., ‘Phase retrieval, what’s new’, SIAG/OPT Views and News 25(1) (2017), 1–5.Google Scholar
Matoušková, E. and Reich, S., ‘The Hundal example revisited’, J. Nonlinear Convex Anal. 4(3) (2003), 411–427.Google Scholar
Moursi, W. M., ‘The Douglas–Rachford operator in the possibly inconsistent case: static properties and dynamic behaviour’, PhD Thesis, University of British Columbia, (2016).Google Scholar
Moursi, W. M. and Vandenberghe, L., ‘Douglas–Rachford splitting for a Lipschitz continuous and a strongly monotone operator’, Preprint, (2018), arXiv:1805.09396.Google Scholar
Moursi, W. M. and Zinchenko, Y., ‘A note on the equivalence of operator splitting methods’, in: Splitting Algorithms, Modern Operator Theory, and Applications (Springer, 2019), 331–349.Google Scholar
Needham, T., Visual Complex Analysis (Oxford University Press, 1997).Google Scholar
Patrinos, P., Stella, L. and Bemporad, A., ‘Douglas–Rachford splitting: Complexity estimates and accelerated variants’, in: 53rd IEEE Conference on Decision and Control, Los Angeles, CA, 15–17 December, 2014 (IEEE, 2014), 4234–4239.Google Scholar
Peaceman, D. W. and Rachford, H. H. Jr, ‘The numerical solution of parabolic and elliptic differential equations’, J. Soc. Ind. Appl. Math. 3(1) (1955), 28–41.Google Scholar
Phan, H. M., ‘Linear convergence of the Douglas–Rachford method for two closed sets’, Optimization 65(2) (2016), 369–385.Google Scholar
Pierra, G., ‘Decomposition through formalization in a product space’, Math. Program. 28(1) (1984), 96–115.Google Scholar
Rockafellar, R. T., Conjugate Duality and Optimization, Regional Conference Series in Applied Mathematics, 16 (SIAM, 1976).Google Scholar
Rockafellar, R. T., ‘Monotone operators and the proximal point algorithm’, SIAM J. Control Optim. 14(5) (1976), 877–898.Google Scholar
Schaad, J., ‘Modeling the 8-queens problem and sudoku using an algorithm based on projections onto nonconvex sets’, PhD Thesis, University of British Columbia, (2010).Google Scholar
Setzer, S., ‘Split Bregman algorithm, Douglas–Rachford splitting and frame shrinkage’, in: International Conference on Scale Space and Variational Methods in Computer Vision (Springer, Berlin–Heidelberg, 2009), 464–476.Google Scholar
Spingarn, J. E., ‘Partial inverse of a monotone operator’, Appl. Math. Optim. 10(1) (1983), 247–265.Google Scholar
Steidl, G. and Teuber, T., ‘Removing multiplicative noise by Douglas–Rachford splitting methods’, J. Math. Imag. Vis. 36(2) (2010), 168–184.Google Scholar
Svaiter, B. F., ‘On weak convergence of the Douglas–Rachford method’, SIAM J. Control Opt. 49(1) (2011), 280–287.Google Scholar
Svaiter, B. F., ‘A weakly convergent fully inexact Douglas–Rachford method with relative error tolerance’, ESAIM: COCV 25 (2019), 57 pages.Google Scholar
Tam, M. K., ‘Iterative projection and reflection methods: theory and practice’, PhD Thesis, University of Newcastle, (2016).Google Scholar
Themelis, A. and Patrinos, P., ‘Douglas–Rachford splitting and ADMM for nonconvex optimization: tight convergence results’, (2018).Google Scholar
von Neumann, J., Functional Operators, Vol. II (Oxford University Press, 1950), a reprint of mimeographed notes first distributed in 1933.Google Scholar
Wang, F., Reid, G. and Wolkowicz, H., ‘Finding maximum rank moment matrices by facial reduction on primal form and Douglas–Rachford iteration’, ACM Commun. Comput. Algebra 51(1) (2017), 35–37.Google Scholar
Zarantonello, E. H., ‘Projections on convex sets in Hilbert space and spectral theory: Part I. Projections on convex sets: Part II. Spectral theory.’, in: Contributions to Nonlinear Functional Analysis (Academic Press, 1971), 237–424.Google Scholar