Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Even-Dar Mandel, S.
and
Lifshitz, R.
2008.
Electronic energy spectra of square and cubic Fibonacci quasicrystals.
Philosophical Magazine,
Vol. 88,
Issue. 13-15,
p.
2261.
Dekking, Michel
2009.
Fractal Geometry and Stochastics IV.
Vol. 61,
Issue. ,
p.
269.
PERES, YUVAL
and
SHMERKIN, PABLO
2009.
Resonance between Cantor sets.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 1,
p.
201.
Anisca, Razvan
and
Chlebovec, Christopher
2009.
On the structure of arithmetic sums of Cantor sets with constant ratios of dissection.
Nonlinearity,
Vol. 22,
Issue. 9,
p.
2127.
Rafe Jones
2011.
Achievement Sets of Sequences.
The American Mathematical Monthly,
Vol. 118,
Issue. 6,
p.
508.
Glendinning, Paul
2014.
Invariant Measures for the n-Dimensional Border Collision Normal Form.
International Journal of Bifurcation and Chaos,
Vol. 24,
Issue. 12,
p.
1450164.
Belegradek, Igor
and
Jiang, Zixin
2017.
Smoothness of Minkowski sum and generic rotations.
Journal of Mathematical Analysis and Applications,
Vol. 450,
Issue. 2,
p.
1229.
Shmerkin, Pablo
2019.
On the Hausdorff dimension of pinned distance sets.
Israel Journal of Mathematics,
Vol. 230,
Issue. 2,
p.
949.
Athreya, Jayadev S.
Reznick, Bruce
and
Tyson, Jeremy T.
2019.
Cantor Set Arithmetic.
The American Mathematical Monthly,
Vol. 126,
Issue. 1,
p.
4.
Menceur, Mohamed
and
Mabrouk, Anouar Ben
2019.
A joint multifractal analysis of vector valued non Gibbs measures.
Chaos, Solitons & Fractals,
Vol. 126,
Issue. ,
p.
203.
Behme, Anita
Lindner, Alexander
Reker, Jana
and
Rivero, Victor
2021.
Continuity properties and the support of killed exponential functionals.
Stochastic Processes and their Applications,
Vol. 140,
Issue. ,
p.
115.
Feng, De‐Jun
and
Wu, Yu‐Feng
2021.
On arithmetic sums of fractal sets in Rd.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 1,
p.
35.
Marchese, L.
2022.
On the measure of products from the middle-third Cantor set.
Acta Mathematica Hungarica,
POURBARAT, MEHDI
2023.
Topological structure of the sum of two homogeneous Cantor sets.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 5,
p.
1712.
Lutz, Jack H.
Qi, Renrui
and
Yu, Liang
2024.
The Point-to-Set Principle and the dimensions of Hamel bases.
Computability,
Vol. 13,
Issue. 2,
p.
105.


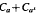 is an interval if and only if a /(1−2
is an interval if and only if a /(1−2