Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T19:21:32.871Z Has data issue: false hasContentIssue false
  • English
  • Français

A subspace theorem for ordinary linear differential equations

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  09 April 2009

Alice Ann Miller
Alice Ann Miller
Affiliation:
University of Western AustraliaNedlands WA 6009, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The study of the S-unit equation for algebraic numbers rests very heavily on Schmidt's Subspace Theorem. Here we prove an effective subspace theorem for the differential function field case, which should be valuable in the proof of results concerning the S-unit equation for function fields. Theorem 1 states that either 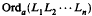has a given upper bound where 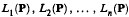are linearly independent linear forms in the polynomials 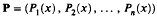with coefficients that are formal power series solutions about x = 0 of non-zero differential equations and where Orda denotes the order of vanishing about a regular (finite) point of functions ƒk, i: (k = 1, n; i = 1, n) or 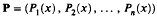lies inside one of a finite number of proper subspaces of (K(x))n. The proof of the theorem is based on the wroskian methods and graded sub-rings of Picard-Vessiot extensions developed by D. V. Chudnovsky and G. V. Chudnovsky in their function field analogues of the Roth and Schmidt theorems. A brief discussion concerning the possibility of a subspace theorem for a product of valuations including the infinite one is also included.

MSC classification

Secondary: 11J61: Approximation in non-Archimedean valuations 11J82: Measures of irrationality and of transcendence
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 50 , Issue 2 , April 1991 , pp. 320 - 332
Copyright
Copyright © Australian Mathematical Society 1991

References

[1]Chudnovsky, D. V. and Chudnovsky, G. V., ‘Rational approximations to solutions of linear differential equations’, Proc. Nat. Acad. Sci. U.S.A. 80 (1983), 5158–5162.CrossRefGoogle ScholarPubMed
[2]Evertse, J. H. and Györy, K., ‘S-unit equations and their applications’, New advances in transcendence theory (Durham, 1986), pp. 110–174, (Cambridge University Press, Cambridge, New York, 1988).Google Scholar
[3]Jacobson, N., Basic algebra II, (Freeman, 1980).Google Scholar
[4]Osgood, C. F., ‘Concerning a possible Thue-Siegel-Roth theorem for algebraic differential equations’, Number theory and algebra, pp. 223–234, (Academic Press, 1977).Google Scholar
[5]Osgood, C. F., ‘Sometimes effective Thue-Siegel-Roth-Schmidt-Nevanlinna bounds, or better’, J. Number Theory 21 (1985), 347–389.CrossRefGoogle Scholar
[6]Roth, K. F., ‘Rational approximations to algebraic numbers’, Mathematika 2 (1955), 1–20.CrossRefGoogle Scholar
[7]Schlickerwei, H. P., ‘On products of special linear forms with algebraic coefficients’, Acta Arith. 31 (1976), 389–398.CrossRefGoogle Scholar
[8]Schmidt, W. M., ‘Diophantine approximations’, Lecture Notes in Mathematics 785, (Springer-Verlag, 1980).Google Scholar