Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T07:40:57.371Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONGLY IRREDUCIBLE IDEALS

Part of: General commutative ring theory Chain conditions, finiteness conditions Arithmetic rings and other special rings Theory of modules and ideals

Published online by Cambridge University Press:  01 April 2008

A. AZIZI
A. AZIZI*
Affiliation:
Department of Mathematics, College of Sciences, Shiraz University, Shiraz 71454, Iran (email: [email protected], [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

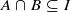A proper ideal I of a ring R is said to be strongly irreducible if for each pair of ideals A and B of R, implies that eithe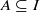r or 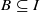. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.

Keywords

absolutely flat ringsarithmetical ringsgeneralizations of Dedekind domainsLaskerian ringsstrongly irreducible idealsZariski topology

MSC classification

Secondary: 13A15: Ideals; multiplicative ideal theory 13C05: Structure, classification theorems 13E05: Noetherian rings and modules 13F99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 2 , April 2008 , pp. 145 - 154
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Atiyah, M. F. and MacDonald, I. G., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
[2]Heinzer, W. J., Ratliff, L. J. Jr and Rush, D. E., ‘Strongly irreducible ideals of a commutative ring’, J. Pure Appl. Algebra 166 (2002), 267–275.CrossRefGoogle Scholar
[3]Jensen, C., ‘Arithmetical rings’, Acta Math. Sci. Acad. Sci. Hungar. 17 (1966), 115–123.CrossRefGoogle Scholar
[4]Larsen, M. D. and McCarthy, P. J., Multiplicative Theory of Ideals (Academic Press, New York, 1971).Google Scholar
[5]Matsumura, H., Commutative Ring Theory (Cambridge University Press, Cambridge, 1992).Google Scholar