Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:01:44.368Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONG SKEW COMMUTATIVITY PRESERVING MAPS ON RINGS

Part of: Radicals and radical properties of rings Conditions on elements

Published online by Cambridge University Press:  25 November 2015

LEI LIU
LEI LIU*
Affiliation:
School of Mathematics and Statistics, Xidian University, Xi’an 710071, PR China School of Mathematical Sciences, Fudan University, Shanghai 200433, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 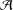${\mathcal{A}}$ be a unital ring with involution. Assume that 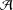${\mathcal{A}}$ contains a nontrivial symmetric idempotent and 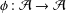${\it\phi}:{\mathcal{A}}\rightarrow {\mathcal{A}}$ is a nonlinear surjective map. We prove that if 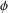${\it\phi}$ preserves strong skew commutativity, then 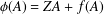${\it\phi}(A)=ZA+f(A)$ for all 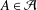$A\in {\mathcal{A}}$, where $Z\in {\mathcal{Z}}_{s}({\mathcal{A}})$ satisfies 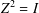$Z^{2}=I$ and 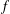$f$ is a map from 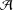${\mathcal{A}}$ into 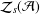${\mathcal{Z}}_{s}({\mathcal{A}})$. Related results concerning nonlinear strong skew commutativity preserving maps on von Neumann algebras are given.

Keywords

strong skew commutativityringsvon Neumann algebras

MSC classification

Primary: 16N60: Prime and semiprime rings
Secondary: 16U80: Generalizations of commutativity
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 1 , February 2016 , pp. 78 - 85
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Beidar, K. I., Martindale, W. S. III and Mikhalev, A. V., Rings with Generalized Identities (Marcel Dekker, New York, Basel, Hong Kong, 1996).Google Scholar
Brešar, M., Chebotar, M. A. and Martindale, W. S. III, Functional Identities (Birkhäuser, Basel, 2007).CrossRefGoogle Scholar
Brešar, M. and Fosňer, M., ‘On ring with involution equipped with some new product’, Publ. Math. Debrecen 57 (2000), 121–134.CrossRefGoogle Scholar
Chebotar, M. A., Fong, Y. and Lee, P.-H., ‘On maps preserving zeros of the polynomial xy − yx ∗’, Linear Algebra Appl. 408 (2005), 230–243.CrossRefGoogle Scholar
Cui, J. and Hou, J., ‘Linear maps preserving elements annihilated by a polynomial XY− YX †’, Studia Math. 174 (2006), 183–199.CrossRefGoogle Scholar
Cui, J. and Park, C., ‘Maps preserving strong skew Lie product on factor von Neumann algebras’, Acta Math. Sci. Ser. B 32 (2012), 531–538.Google Scholar
Hungerford, T. W., Algebra (Springer, Berlin, Heidelberg, New York, 1974).Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, Vols. I, II (Academic Press, New York, 1983, 1986).Google Scholar
Miers, C. R., ‘Lie isomorphisms of operator algebras’, Pacific J. Math. 38 (1971), 717–735.CrossRefGoogle Scholar
Molnár, L., ‘A condition for a subspace of B (H) to be an ideal’, Linear Algebra Appl. 235 (1996), 229–234.CrossRefGoogle Scholar
Qi, X. and Hou, J., ‘Strong skew commutativity preserving maps on von Neumann algebras’, J. Math. Anal. Appl. 397 (2013), 362–370.CrossRefGoogle Scholar
Šemrl, P., ‘On Jordan ∗-derivations and an application’, Colloq. Math. 59 (1990), 241–251.CrossRefGoogle Scholar
Šemrl, P., ‘Quadratic functionals and Jordan ∗-derivations’, Studia Math. 97 (1991), 157–265.CrossRefGoogle Scholar
Šemrl, P., ‘Quadratic and quasi-quadratic functionals’, Proc. Amer. Math. Soc. 119 (1993), 1105–1113.CrossRefGoogle Scholar
Šemrl, P., ‘Jordan ∗-derivations of standard operator algebras’, Proc. Amer. Math. Soc. 120 (1994), 515–519.Google Scholar