Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T19:20:54.359Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME WEAKER FORMS OF THE CHAIN (F) CONDITION FOR METACOMPACTNESS

Part of: Fairly general properties

Published online by Cambridge University Press:  01 April 2008

ÇETIN VURAL
ÇETIN VURAL*
Affiliation:
Gazi Universitesi, Fen-Edebiyat Fakultesi Matematik Bolumu, 06500 Teknikokullar, Ankara, Turkey (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define, in a slightly unusual way, the rank of a partially ordered set. Then we prove that if X is a topological space and 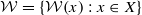satisfies condition (F) and, for every x∈X, 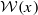is of the form 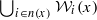, where 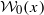is Noetherian of finite rank, and every other 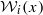is a chain (with respect to inclusion) of neighbourhoods of x, then X is metacompact. We also obtain a cardinal extension of the above. In addition, we give a new proof of the theorem ‘if the space X has a base 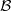of point-finite rank, then X is metacompact’, which was proved by Gruenhage and Nyikos.

Keywords

point-countablemetacompactrankNoetherianrefinement

MSC classification

Secondary: 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 2 , April 2008 , pp. 283 - 288
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Collins, P. J., Reed, G. M., Roscoe, A. W. and Rudin, M. E., ‘A lattice of conditions on topological spaces’, Proc. Amer. Math. Soc. 94 (1985), 487–496.CrossRefGoogle Scholar
[2]Dilworth, R. P., ‘A decomposition theorem for partially ordered sets’, Ann. Math. 51 (1950), 161–166.CrossRefGoogle Scholar
[3]Erdös, P., Hajnal, A., Mate, A. and Rado, R., Combinatorial Set Theory: Partition Relations for Cardinals (North-Holland, Amsterdam, 1984).Google Scholar
[4]Gartside, P. M. and Moody, P. J., ‘Well-ordered (F) spaces’, Topology Proc. 17 (1992), 111–130.Google Scholar
[5]Gruenhage, G. and Nyikos, P., ‘Spaces with bases of countable rank’, Topology Appl. 8 (1978), 233–257.CrossRefGoogle Scholar
[6]Moody, P. J., Reed, G. M., Roscoe, A. W. and Collins, P. J., ‘A lattice condition on topological spaces II’, Fund. Math. 138 (1991), 69–81.CrossRefGoogle Scholar
[7]Morita, K. and Nagata, J., Topics in General Topology (North-Holland, Amsterdam, 1989).Google Scholar