Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-23T16:20:46.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Uniqueness Theorems for Functional Equations

Published online by Cambridge University Press:  09 April 2009

T. D. Howroyd
T. D. Howroyd
Affiliation:
University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized Pexider equation 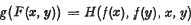where f and g are unknown and x, y, are real, has been discussed by J. Aczél [1] and J. Aczé and M. Hosszú [2]. In [2] it is shown that if F is continuous and F and H are strictly increasing in their first variables and strictly decreasing in their second variables, then two initial conditions suffice to determine at most one continuous solution f of (1). We extend these results to strictly increasing and strictly decreasing functions F and derive results for strictly monotonic F and H.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 1-2 , February 1969 , pp. 176 - 179
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Aczél, J., ‘Ein Eindeutigkeitssatz in der Theorie der Funktional-gleichungen und einige ihrer Anwendungen’, Acta Math. Acad. Sci. Hung. 15 (1964), 355–362.CrossRefGoogle Scholar
[2]Aczél, J. and Hosszú, M., ‘Further Uniqueness Theorems for Functional Equations’, Acta Math. Acad. Sci. Hung. 16 (1965), 51–55.CrossRefGoogle Scholar