Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T08:40:20.296Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results on the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments

Part of: Functional-differential and differential-difference equations Qualitative theory

Published online by Cambridge University Press:  09 April 2009

Ch. G. Philos ,
Y. G. Sficas  and
V. A. Staikos
Ch. G. Philos
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Y. G. Sficas
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
V. A. Staikos
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with some asymptotic properties of nonoscillatory solutions of a class of n-th order (n < 1) differential equations with deviationg arguments involving the so called n-th order r-derivative of the unknown function x defined by

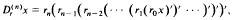
where ri (i = 0,1…n) are positive continous functions on [t0, ∞). The fundamental purpose of this paper is to find for any integer m, 0 < m < n – 1, a necessary and sufficient condition (depending on m) in order that three exists at least one (nonoscillatory) solution x so that the 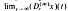exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).

MSC classification

Secondary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory 34K25: Asymptotic theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 32 , Issue 3 , June 1982 , pp. 295 - 317
Copyright
Copyright © Australian Mathematical Society 1982

References

Coffman, C. V. and Wong, J. S. W. (1972), ‘Oscillation and nonoscillation theorems for second order ordinary differential equations’, Funkcional. Ekvac. 15, 119–130.Google Scholar
Coppel, W. A. (1971), Disconjugacy, Lecture Notes in Mathematics 220 (Springer-Verlag).CrossRefGoogle Scholar
Grammatikopoulos, M. K., Sficas, Y. G. and Staikos, V. A. (1978), ‘Asymptotic and oscillatory criteria for retarded differential equations’, J. Math. Anal. Appl. 63, 591–605.CrossRefGoogle Scholar
Kusano, T. and Onose, H. (1975), ‘Nonoscillatory solutions of differential equations with retarded arguments’, Bull. Fac. Sci. Ibaraki Univ. Ser. A 7, 1–11.CrossRefGoogle Scholar
Kusano, T. and Onose, H. (1976a), ‘Asymptotic behavior of nonoscillatory solutions of functional differential equations of arbitrary order’, J. London Math. Soc. 14, 106–112.CrossRefGoogle Scholar
Kusano, T. and Onose, H. (1976b), ‘Nonoscillation theorems for differential equations with deviating argument’, Pacific J. Math. 63, 185–192.CrossRefGoogle Scholar
Ladas, G. (1971), ‘Oscillation and asymptotic behavior of solutions of differential equations with retarded argument’, J. Differential Equations 10, 281–290.CrossRefGoogle Scholar
Marušiak, P. (1973), ‘Note on the Ladas' paper on oscillation and asymptotic behavior of solutions of differential equations with retarded argument’, J. Differential Equations 13, 150–156.CrossRefGoogle Scholar
Onose, H. (1973), ‘Oscillation and asymptotic behavior of solutions of retarded differential equations of arbitrary order’, Hiroshima Math. J. 3, 333–360.CrossRefGoogle Scholar
Philos, Ch. G. (1977), ‘An oscillatory and asymptotic classification of the solutions of differential equations with deviating arguments’, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 63, 195–203.Google Scholar
Philos, Ch. G. (1978a), ‘Oscillatory and asymptotic behavior of the bounded solutions of differential equations with deviating arguments’, Hiroshima Math. J. 8, 31–48.CrossRefGoogle Scholar
Philos, Ch.G. (1978b), ‘Oscillatory and asymptotic behavior of all solutions of differential equations with deviating arguments’, Proc. Roy. Soc. Edinburgh Sect. A 81, 195–210.CrossRefGoogle Scholar
Philos, Ch. G. and Staikos, V. A. (1979), ‘Quick oscillations with damping’, Math. Nachr. 92, 153–160.CrossRefGoogle Scholar
Philos, Ch. G. and Staikos, V. A. (1980), ‘Non-slow oscillations with damping’, Rev. Roum. Math. Pures Appl. 25, 1099–1110.Google Scholar
Schauder, J. (1930), ‘Der Fixpunktsatz in Functionalräumen’, Studia Math. 2, 171–180.CrossRefGoogle Scholar
Staikos, V. A. (1976), Differential equations with deviating arguments-oscillation theory, unpublished.Google Scholar
Staikos, V. A. and Philos, Ch. G. (1977a), ‘On the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments’, Hiroshima Math. J. 7, 9–31.Google Scholar
Staikos, V. A. and Philos, Ch. G. (1977b), ‘Asymptotic properties of nonoscillatory solutions of differential equations with deviating argument’, Pacific J. Math. 70, 221–242.Google Scholar
Staikos, V. A. and Philos, Ch. G. (1978), ‘Nonoscillatory phenomena and damped oscillations’, Nonlinear Anal. 2, 197–210.CrossRefGoogle Scholar
Staikos, V. A. and Sficas, Y. G. (1972), ‘Criteria for asymptotic and oscillatory character of functional differential equations of arbitrary order’, Boll. Un. Mat. Ital. 6, 185–192.Google Scholar
Trench, W. F. (1975), ‘Oscillation properties of perturbed disconjugate equations’, Proc. Amer. Math. Soc. 52, 147–155.CrossRefGoogle Scholar
Tychonoff, A. (1935), ‘Ein Fixpunktsatz,’ Math. Ann. 111, 767–776.CrossRefGoogle Scholar