Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wall, G. E.
1962.
On the Clifford Collineation, Transform and Similarity Groups (IV): An Application to Quadratic Forms.
Nagoya Mathematical Journal,
Vol. 21,
Issue. ,
p.
199.
Blachman, N.
1962.
On the capacity of a band-limited channel perturbed by statistically dependent interference.
IEEE Transactions on Information Theory,
Vol. 8,
Issue. 1,
p.
48.
Fisher, Michael E.
and
Gaunt, David S.
1964.
Ising Model and Self-Avoiding Walks on Hypercubical Lattices and "High-Density" Expansions.
Physical Review,
Vol. 133,
Issue. 1A,
p.
A224.
Scott, P. R.
1966.
The Construction of Perfect and Extreme Forms.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
147.
Leech, John
1967.
Notes on Sphere Packings.
Canadian Journal of Mathematics,
Vol. 19,
Issue. ,
p.
251.
1969.
Geometry of Numbers.
p.
471.
Bos, A.
Conway, J. H.
and
Sloane, N. J. A.
1982.
Further lattice packings in high dimensions.
Mathematika,
Vol. 29,
Issue. 2,
p.
171.
Conway, J. H.
and
Sloane, N. J. A.
1984.
On the Voronoi Regions of Certain Lattices.
SIAM Journal on Algebraic Discrete Methods,
Vol. 5,
Issue. 3,
p.
294.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Forney, G.D.
1988.
Coset codes. II. Binary lattices and related codes.
IEEE Transactions on Information Theory,
Vol. 34,
Issue. 5,
p.
1152.
Gibson, Jerry D.
and
Sayood, Khalid
1988.
Vol. 72,
Issue. ,
p.
259.
Forney, G.D.
1988.
Coset codes. I. Introduction and geometrical classification.
IEEE Transactions on Information Theory,
Vol. 34,
Issue. 5,
p.
1123.
Calderbank, A.R.
1989.
Multilevel codes and multistage decoding.
IEEE Transactions on Communications,
Vol. 37,
Issue. 3,
p.
222.
Chen, T.-C.
1990.
A lattice vector quantization using a geometric decomposition.
IEEE Transactions on Communications,
Vol. 38,
Issue. 5,
p.
704.
Hahn, Alexander J.
1990.
The Coset lattices of E. S. Barnes and G. E. Wall.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 49,
Issue. 3,
p.
418.
Buser, P.
and
Sarnak, P.
1994.
On the period matrix of a Riemann surface of large genus (with an Appendix by J.H. Conway and N.J.A. Sloane).
Inventiones Mathematicae,
Vol. 117,
Issue. 1,
p.
27.
Ericson, T.
and
Zinoviev, V.
1995.
Spherical codes generated by binary partitions of symmetric pointsets.
IEEE Transactions on Information Theory,
Vol. 41,
Issue. 1,
p.
107.
Horváth, Ákos G.
1995.
On the sublattices of the Barnes-wall lattice.
Periodica Mathematica Hungarica,
Vol. 31,
Issue. 2,
p.
131.
Tiep, Pham Huu
1997.
Weil Representations as Globally Irreducible Representations.
Mathematische Nachrichten,
Vol. 184,
Issue. 1,
p.
313.
Scharlau, Rudolf
and
Tiep, Pham Huu
1997.
Symplectic Groups, Symplectic Spreads, Codes, and Unimodular Lattices.
Journal of Algebra,
Vol. 194,
Issue. 1,
p.
113.


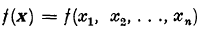 be a positive definite quadratic form of determinant
be a positive definite quadratic form of determinant 

