Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T08:38:28.571Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME COVERS AND ENVELOPES IN THE CHAIN COMPLEX CATEGORY OF R-MODULES

Part of: Homological algebra Model theory

Published online by Cambridge University Press:  31 August 2011

ZHANPING WANG  and
ZHONGKUI LIU
ZHANPING WANG*
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, PR China (email: [email protected])
ZHONGKUI LIU
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, PR China (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of some covers and envelopes in the chain complex category of R-modules. Let (𝒜,ℬ) be a cotorsion pair in R-Mod and let ℰ𝒜 stand for the class of all exact complexes with each term in 𝒜. We prove that (ℰ𝒜,ℰ𝒜⊥) is a perfect cotorsion pair whenever 𝒜 is closed under pure submodules, cokernels of pure monomorphisms and direct limits and so every complex has an ℰ𝒜-cover. As an application we show that every complex of R-modules over a right coherent ring R has an exact Gorenstein flat cover. In addition, the existence of 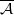-covers and 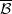-envelopes of special complexes is considered where 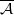and 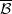denote the classes of all complexes with each term in 𝒜 and ℬ, respectively.

Keywords

cotorsion paircoverenvelopeGorenstein flat complex

MSC classification

Secondary: 18G35: Chain complexes 03C35: Categoricity and completeness of theories
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 90 , Issue 3 , June 2011 , pp. 385 - 401
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

Supported by the National Natural Science Foundation of China (10961021).

References

[1]Aldrich, S. T., Enochs, E. E., García Rozas, J. R. and Oyonarte, L., ‘Covers and envelopes in Grothendieck categories: flat covers of complexes with applications’, J. Algebra 243 (2001), 615–630.CrossRefGoogle Scholar
[2]Anderson, F. W. and Fuller, K. R., Rings and Categories of Modules (Springer, Berlin, 1992).CrossRefGoogle Scholar
[3]Eklof, P. C. and Trlifaj, J., ‘How to make Ext vanish’, Bull. Lond. Math. Soc. 33 (2001), 41–51.CrossRefGoogle Scholar
[4]Enochs, E. E., ‘Injective and flat covers, envelopes and resolvents’, Israel J. Math. 39 (1981), 189–209.CrossRefGoogle Scholar
[5]Enochs, E. E. and García Rozas, J. R., ‘Tensor products of complexes’, Math. J. Okayama Univ. 39 (1997), 17–39.Google Scholar
[6]Enochs, E. E. and García Rozas, J. R., ‘Gorenstein injective and projective complexes’, Comm. Algebra 26 (1998), 1657–1674.CrossRefGoogle Scholar
[7]Enochs, E. E. and García Rozas, J. R., ‘Flat covers of complexes’, J. Algebra 210 (1998), 86–102.CrossRefGoogle Scholar
[8]Enochs, E. E. and Jenda, O. M. G., Relative Homological Algebra (Walter de Gruyter, Berlin, 2000).CrossRefGoogle Scholar
[9]Enochs, E. E., Jenda, O. M. G. and López Ramos, J. A., ‘The existence of Gorenstein flat covers’, Math. Scand. 94 (2004), 46–62.CrossRefGoogle Scholar
[10]Enochs, E. E., Jenda, O. M. G. and Torrecillas, B., ‘Gorenstein flat modules’, Nanjing Univ. J. Math. Biquarterly 1 (1993), 1–9.Google Scholar
[11]Enochs, E. E., Jenda, O. M. G. and Xu, J., ‘Orthogonality in the category of complexes’, Math. J. Okayama Univ. 38 (1996), 25–46.Google Scholar
[12]Enochs, E. E. and López Ramos, J. A., Gorenstein Flat Modules (Nova Science, New York, 2001).Google Scholar
[13]García Rozas, J. R., Covers and Envelopes in the Category of Complexes of Modules (CRC Press, Boca Raton, FL, 1999).Google Scholar
[14]Gillespie, J., ‘The flat model structure on Ch(R)’, Trans. Amer. Math. Soc. 356 (2004), 3369–3390.CrossRefGoogle Scholar
[15]Gillespie, J., ‘Kaplansky classes and derived categories’, Math. Z. 257 (2007), 811–843.CrossRefGoogle Scholar
[16]Gillespie, J., ‘Cotorsion pairs and degreewise homological model structures’, Homology, Homotopy Appl. 10 (2008), 283–304.CrossRefGoogle Scholar
[17]Göbel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules (Walter de Gruyter, Berlin, 2006).CrossRefGoogle Scholar
[18]Holm, H., ‘Gorenstein homological dimensions’, J. Pure Appl. Algebra 189 (2004), 167–193.CrossRefGoogle Scholar
[19]Hovey, M., ‘Cotorsion theories, model category structures, and representation theory’, Math. Z. 241 (2002), 553–592.CrossRefGoogle Scholar
[20]Mao, L. X., ‘Min-flat modules and min-coherent rings’, Comm. Algebra 35 (2007), 635–650.CrossRefGoogle Scholar
[21]Mao, L. X. and Ding, N. Q., ‘Envelopes and covers by modules of finite FP-injective and flat dimensions’, Comm. Algebra 35 (2007), 833–849.CrossRefGoogle Scholar
[22]Salce, L., ‘Cotorsion theories for abelian groups’, in: Symposia Mathematica XXIII. 1979, pp. 11–32.Google Scholar
[23]Wang, Z. P., ‘Researches of relative homological properties in the category of complexes’, PhD Thesis, Northwest Normal University, 2010.Google Scholar
[24]Xu, J. Z., Flat Covers of Modules, Lecture Notes in Mathematics, 1634 (Springer, Berlin, 1996).CrossRefGoogle Scholar