Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-12T12:19:38.945Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Classes of Indecomposable Varieties of Groups

Published online by Cambridge University Press:  09 April 2009

John Cossey
John Cossey
Affiliation:
Graduate Center The City University of New York New York, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A variety of groups is an equationally defined class of groups: equivalently, it is a class of groups closed under the operations of taking cartesian products, subgroups, and quotient groups. If and 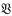are varieties, then 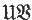is the class of all groups G with a normal subgroup N in such that G/N is in 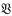; 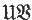is a variety, called the product of and 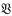. We denote by the variety generated by the unit group, and by 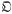the variety of all groups. We say that a variety 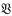is indecomposable if , and 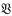cannot be written as a product 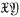, with both 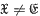and 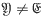One of the basic results in the theory of varieties of groups is that the set of varieties, excluding 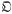, and with multiplication of varieties as above, is a free semi-group, freely generated by the indecomposable varieties. Thus one would like to be able to decide whether a given variety is indecomposable or not. In connection with this question, Hanna Neumann raises the following problem (as part of Problem 7 in her book [7]): Problem 1. If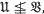andprove that [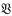] is indecomposable unless bothand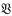have a common non-trivial right hand factor.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 3-4 , May 1969 , pp. 387 - 398
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Baumslag, Gilbert, ‘Some subgroup theorems for free v-groups’, Trans. Amer. Math. Soc. 108 (1963), 516–525.Google Scholar
[2]Cossey, John, ‘Laws in nilpotent-by-finite groups’, Proc. Amer. Math. Soc. (to appear).Google Scholar
[3]Gaschutz, W., ‘Endliche Gruppen mit treuen absolut-irreduziblen Darstellungen’, Math. Nachr. 12 (1954), 253–255.CrossRefGoogle Scholar
[4]Hall, P., ‘Finite-by-nilpotent groups’, Proc. Cambridge Phil. Soc. 52 (1956), 611–616.CrossRefGoogle Scholar
[5]Hall, P., ‘On the finiteness of certain soluble groups’, Proc. London Math. Soc. Ser. 3. 9 (1959), 595–622.CrossRefGoogle Scholar
[6]Liebeck, Hans, ‘Concerning nilpotent wreath products’, Proc. Cambridge Phil. Soc. 58 (1962), 443–451.CrossRefGoogle Scholar
[7]Neumann, Hanna, Varieties of groups. Ergebnisse der Mathematik und ihrer Grenzgebiete, Bd 37, Springer, Berlin, 1967.Google Scholar
[8]Neumann, B. H., ‘Identical relations in groups I’, Math. Ann. 114 (1937), 506–525.CrossRefGoogle Scholar
[9]Newman, M. F., ‘On a class of nilpotent groups’, Proc.. London Math. Soc. 3. 10 (1960), 365–375.CrossRefGoogle Scholar
[10]Newman, M. F., ‘On a class of metabelian groups’, Proc London Math. Soc. 3. 10 (1960), 354–364.CrossRefGoogle Scholar
[11]Redei, L., ‘Die endlichen einstufig nichtnilpotenten Gruppen’, Publ. Math. Debrecen 4 (1956), 130–138.Google Scholar