No CrossRef data available.
Article contents
Sequences of integers satisfying congruence relations and Pisot-Vijayaraghavan numbers
Published online by Cambridge University Press: 09 April 2009
Extract
We consider infinite sequences 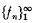 of positive integers having exponential growth:
of positive integers having exponential growth: 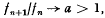 and becoming ultimately periodic modulo each member of a rather sparse infinite set of integers. If sufficient, natural conditions are placed on the growth and periodicities of
and becoming ultimately periodic modulo each member of a rather sparse infinite set of integers. If sufficient, natural conditions are placed on the growth and periodicities of 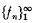 , we find that a is an algebraic integer having all its algebraic conjugates within or on the unit circle, and fn has a special representation involving an. The result is a kind of dual to the theorem of Pisot (cf. Salem [2], p. 4, Theorem A).
, we find that a is an algebraic integer having all its algebraic conjugates within or on the unit circle, and fn has a special representation involving an. The result is a kind of dual to the theorem of Pisot (cf. Salem [2], p. 4, Theorem A).
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1967


