Article contents
Separation axioms and subcategories of top
Published online by Cambridge University Press: 09 April 2009
Abstract
(Point, closed subset)-separation axioms and closed subsets separation axioms for topological spaces will be uniformly defined. Then it is shown that a subcategory 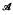 of TOP is bireflective in TOP if and only if Ob
of TOP is bireflective in TOP if and only if Ob 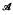 consists of all separated spaces for some (point, closed subset)-separation axiom. A characterization theorem on subcategories of all separated spaces for closed subsets separation axioms is also given by using the category SEP of all separation spaces and the embedding functor G: TOP → SEP. As an application we have that a T1-space is normal if and only if it is embedded in a product space of the unit intervals in SEP.
consists of all separated spaces for some (point, closed subset)-separation axiom. A characterization theorem on subcategories of all separated spaces for closed subsets separation axioms is also given by using the category SEP of all separation spaces and the embedding functor G: TOP → SEP. As an application we have that a T1-space is normal if and only if it is embedded in a product space of the unit intervals in SEP.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 22 , Issue 4 , December 1976 , pp. 476 - 490
- Copyright
- Copyright © Australian Mathematical Society 1976
References
- 2
- Cited by


