Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-17T14:01:39.788Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMIRING AND INVOLUTION IDENTITIES OF POWER GROUPS

Part of: Varieties Generalizations Semigroups

Published online by Cambridge University Press:  17 January 2023

SERGEY V. GUSEV Open the ORCID record for SERGEY V. GUSEV [Opens in a new window]  and
MIKHAIL V. VOLKOV Open the ORCID record for MIKHAIL V. VOLKOV [Opens in a new window]
SERGEY V. GUSEV
Affiliation:
Institute of Natural Sciences and Mathematics, Ural Federal University, 620000 Ekaterinburg, Russia e-mail: [email protected]
MIKHAIL V. VOLKOV*
Affiliation:
Institute of Natural Sciences and Mathematics, Ural Federal University, 620000 Ekaterinburg, Russia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For every group G, the set 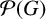$\mathcal {P}(G)$ of its subsets forms a semiring under set-theoretical union $\cup $ and element-wise multiplication $\cdot $, and forms an involution semigroup under $\cdot $ and element-wise inversion 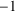${}^{-1}$. We show that if the group G is finite, non-Dedekind, and solvable, neither the semiring 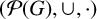$(\mathcal {P}(G),\cup ,\cdot )$ nor the involution semigroup 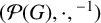$(\mathcal {P}(G),\cdot ,{}^{-1})$ admits a finite identity basis. We also solve the finite basis problem for the semiring of Hall relations over any finite set.

Keywords

additively idempotent semiringfinite basis problempower semiringpower groupblock-groupHall relationBrandt monoidinvolution semigroup

MSC classification

Primary: 16Y60: Semirings
Secondary: 20M18: Inverse semigroups 08B05: Equational logic, Mal′cev (Mal′tsev) conditions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 115 , Issue 3 , December 2023 , pp. 354 - 374
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by James East

Supported by the Russian Science Foundation (grant No. 22-21-00650).

References

Almeida, J., Finite Semigroups and Universal Algebra, Series in Algebra, 3 (World Scientific, Singapore, 1995).10.1142/2481CrossRefGoogle Scholar
Auinger, K., Dolinka, I. and Volkov, M. V., ‘Matrix identities involving multiplication and transposition’, J. Eur. Math. Soc. (JEMS) 14 (2012), 937–969.10.4171/JEMS/323CrossRefGoogle Scholar
Auinger, K., Dolinka, I. and Volkov, M. V., ‘Equational theories of semigroups with involution’, J. Algebra 369 (2012), 203–225.10.1016/j.jalgebra.2012.06.021CrossRefGoogle Scholar
Broshi, A. M., ‘Finite groups whose Sylow subgroups are abelian’, J. Algebra 17 (1971), 74–82.CrossRefGoogle Scholar
Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Vol. I, Mathematical Surveys and Monographs, 7(I) (American Mathematical Society, Providence, RI, 1961).Google Scholar
Dolinka, I., ‘A class of inherently nonfinitely based semirings’, Algebra Universalis 60 (2009), 19–35.10.1007/s00012-008-2084-yCrossRefGoogle Scholar
Dolinka, I., ‘On identities of finite involution semigroups’, Semigroup Forum 80 (2010), 105–120.10.1007/s00233-009-9193-6CrossRefGoogle Scholar
Dolinka, I., ‘Power semigroups of finite groups and the INFB property’, Algebra Universalis 63 (2010), 239–242.10.1007/s00012-010-0075-2CrossRefGoogle Scholar
FitzGerald, D. G., ‘On inverses of products of idempotents in regular semigroups’, J. Aust. Math. Soc. 13 (1972), 335–337.10.1017/S1446788700013756CrossRefGoogle Scholar
Gaysin, A. M. and Volkov, M. V., ‘Block-groups and Hall relations’, in: Semigroups, Categories, and Partial Algebras, Springer Proceedings in Mathematics and Statistics, 345 (eds. Romeo, P. G., Volkov, M. V. and Rajan, A. R.) (Springer, Singapore, 2021), 25–32.10.1007/978-981-33-4842-4_3CrossRefGoogle Scholar
Gusev, S. V. and Volkov, M. V., ‘Semiring identities of finite inverse semigroups’, Semigroup Forum (to appear), see also Preprint, 2022, arXiv:2204.10514v2.CrossRefGoogle Scholar
Hall, M. Jr, The Theory of Groups (Macmillan, New York, 1959).Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Clarendon Press, Oxford, 1995).10.1093/oso/9780198511946.001.0001CrossRefGoogle Scholar
Jackson, M., Ren, M. and Zhao, X., ‘Nonfinitely based ai-semirings with finitely based semigroup reducts’, J. Algebra 611 (2022), 211–245.CrossRefGoogle Scholar
Janko, Z., ‘A new finite simple group with abelian Sylow 2-subgroups and its characterization’, J. Algebra 3 (1966), 147–186.10.1016/0021-8693(66)90010-XCrossRefGoogle Scholar
Ježek, J., Kepka, T. and Maróti, M., ‘The endomorphism semiring of a semilattice’, Semigroup Forum 78 (2009), 21–26.10.1007/s00233-008-9045-9CrossRefGoogle Scholar
Jipsen, P., ‘Relation algebras, idempotent semirings and generalized bunched implication algebras’, in: Relational and Algebraic Methods in Computer Science, Lecture Notes in Computer Science, 10226 (eds. Höfner, P., Pous, D. and Struth, G.) (Springer, Cham, 2017), 144–158.CrossRefGoogle Scholar
Kad’ourek, J., ‘On bases of identities of finite inverse semigroups with solvable subgroups’, Semigroup Forum 67 (2003), 317–343.CrossRefGoogle Scholar
Lee, E. W. H., ‘Equational theories of unstable involution semigroups,’ Electron. Res. Announc. Math. Sci. 24 (2017), 10–20.Google Scholar
Margolis, S. W. and Pin, J.-É., ‘Varieties of finite monoids and topology for the free monoid’, in: Proceedings of the 1984 Marquette Conference on Semigroups (eds. Byleen, K., Jones, P. and Pastijn, F.) (Marquette University, Milwaukee, 1985), 113–129.Google Scholar
Mogiljanskaja, E. M., ‘The solution to a problem of Tamura’, in: Modern Analysis and Geometry (eds. I. Ya. Bakelman et al.) (Leningrad. Gos. Ped. Inst., Leningrad, 1972), 148–151 (in Russian).Google Scholar
Mogiljanskaja, E. M., ‘Non-isomorphic semigroups with isomorphic semigroups of subsets’, Semigroup Forum 6 (1973), 330–333.10.1007/BF02389140CrossRefGoogle Scholar
Montague, J. S. and Plemmons, R. J., ‘Maximal subgroups of the semigroup of relations’, J. Algebra 13 (1969), 575–587.10.1016/0021-8693(69)90119-7CrossRefGoogle Scholar
Pin, J.-É., ‘Variétés de langages et monoïde des parties’, Semigroup Forum 20 (1980), 11–47 (in French).10.1007/BF02572667CrossRefGoogle Scholar
Pin, J.-É., ‘ $\mathrm{BG}=\mathrm{PG}$ , a success story’, in: Semigroups, Formal Languages and Groups, Nato Science Series C, 466 (ed. Fountain, J.) (Kluwer Academic Publishers, Dordrecht–Boston–London, 1995), 33–47.10.1007/978-94-011-0149-3_2CrossRefGoogle Scholar
Pin, J.-É., ‘Tropical semirings’, in: Idempotency, Publications of the Newton Institute, 11 (ed. Gunawardena, J.) (Cambridge University Press, Cambridge, 1998), 50–69.10.1017/CBO9780511662508.004CrossRefGoogle Scholar
Polák, L., ‘Syntactic semiring of a language’, in: Mathematical Foundations of Computer Science 2001, Lecture Notes in Computer Science, 2136 (eds. Sgall, J., Pultr, A. and Kolman, P.) (Springer, Berlin–Heidelberg, 2001), 611–620.10.1007/3-540-44683-4_53CrossRefGoogle Scholar
Polák, L., ‘Syntactic semiring and universal automaton’, In: Developments in Language Theory 2003, Lecture Notes in Computer Science, 2710 (eds. Ésik, Z. and Fülöp, Z.) (Springer, Berlin–Heidelberg, 2003), 411–422.10.1007/3-540-45007-6_33CrossRefGoogle Scholar
Ren, M. and Zhao, X., ‘The varieties of semilattice-ordered semigroups satisfying ${x}^3\approx x$ and ${xy\approx yx}$ ’, Period. Math. Hungar. 72 (2016), 158–170.CrossRefGoogle Scholar
Volkov, M. V., ‘The finite basis problem for finite semigroups’, Sci. Math. Jpn. 53 (2001), 171–199, a periodically updated version is available under http://csseminar.math.ru/MATHJAP_ revisited.pdf.Google Scholar
Volkov, M. V., ‘Semiring identities of the Brandt monoid’, Algebra Universalis 82 (2021), Article no. 42.10.1007/s00012-021-00731-8CrossRefGoogle Scholar