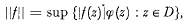Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neville, Charles W.
1972.
Invariant subspaces of Hardy classes on infinitely connected plane domains.
Bulletin of the American Mathematical Society,
Vol. 78,
Issue. 5,
p.
857.
Collins, H.S
1976.
Strict, weighted, and mixed topologies and applications.
Advances in Mathematics,
Vol. 19,
Issue. 2,
p.
207.
Stephenson, Kenneth
1980.
Weak subordination and stable classes of meromorphic functions.
Transactions of the American Mathematical Society,
Vol. 262,
Issue. 2,
p.
565.
Janson, Svante
1980.
Generalizations of Lipschitz spaces and an application to Hardy spaces and bounded mean oscillation.
Duke Mathematical Journal,
Vol. 47,
Issue. 4,
Anderson, J. M.
1985.
Operators and Function Theory.
p.
1.
Shvedenko, S. V.
1987.
Hardy classes and related spaces of analytic functions in the unit circle, polydisc, and ball.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 6,
p.
3011.
Horwitz, Alan L.
and
Rubel, Lee A.
1987.
The space of totally bounded analytic functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 30,
Issue. 2,
p.
229.
Fisher, Stephen D.
1988.
The Möbius Group and Invariant Spaces of Analytic Functions.
The American Mathematical Monthly,
Vol. 95,
Issue. 6,
p.
514.
Anderson, J. M.
and
Duncan, J.
1990.
Duals of Banach spaces of entire functions.
Glasgow Mathematical Journal,
Vol. 32,
Issue. 2,
p.
215.
Anderson, J. M.
Fernández, J. L.
and
Shields, A. L.
1991.
Inner functions and cyclic vectors in the Bloch space.
Transactions of the American Mathematical Society,
Vol. 323,
Issue. 1,
p.
429.
Lusky, Wolfgang
1992.
On the Structure of Hv0(D) and hv0(D).
Mathematische Nachrichten,
Vol. 159,
Issue. 1,
p.
279.
Werner, Dirk
1992.
New classes of Banach spaces which are M-ideals in their biduals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 2,
p.
337.
Bierstedt, K. D.
and
Summers, W. H.
1993.
Biduals of weighted banach spaces of analytic functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
70.
Jarchow, Hans
1995.
SOME FUNCTIONAL ANALYTIC PROPERTIES OF COMPOSITION OPERATORS.
Quaestiones Mathematicae,
Vol. 18,
Issue. 1-3,
p.
229.
Bonet, J.
Domański, P.
Lindström, M.
and
Taskinen, J.
1998.
Composition operators between weighted Banach spaces of analytic functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 64,
Issue. 1,
p.
101.
Contreras, M. D.
and
Hernandez-Diaz, A. G.
2000.
Weighted composition operators in weighted Banach spaces of analytic functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 69,
Issue. 1,
p.
41.
Aleman, Alexandru
Richter, Stefan
and
Sundberg, Carl
2007.
Analytic contractions, nontangential limits, and the index of invariant subspaces.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 7,
p.
3369.
Manhas, J. S.
2007.
Composition Operators and Multiplication Operators on Weighted Spaces of Analytic Functions.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Wolf, Elke
2009.
Differences of weighted composition operators.
Collectanea mathematica,
Vol. 60,
Issue. 1,
p.
1.
Stević, Stevo
and
Wolf, Elke
2009.
Differences of composition operators between weighted-type spaces of holomorphic functions on the unit ball of.
Applied Mathematics and Computation,
Vol. 215,
Issue. 5,
p.
1752.