Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T15:09:35.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Scales of functions

Published online by Cambridge University Press:  09 April 2009

P. Erdös ,
C. A. Rogers  and
S. J. Taylor
P. Erdös
Affiliation:
University College, London The University, Birmingham, 15.
C. A. Rogers
Affiliation:
University College, London The University, Birmingham, 15.
S. J. Taylor
Affiliation:
University College, London The University, Birmingham, 15.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider real-valued functions ƒ(x) which are defined for all sufficiently large real numbers x. In discussing the behaviour of such functions as x → + ∞, it is useful to compare ƒ with the functions of some “comparison scale”. The early work in this field was due to Du Bois-Reymond (see, for example, (2), (3)). This was elaborated by Hardy, (6), who was mainly concerned with what he calls the “logarithmico-exponential” scale of functions. This “scale of Hardy” may be defined as the smallest class ℋ of functions ƒ with the following properties:

(i) if ƒ ∈ ℋ, ƒ, is defined and continuous for all sufficiently large values of x;

(ii) (a) the function ƒ(x) ≡ α, where α is any real constant, is in ℋ;

(b) the function ƒ(x) ≡ x is in ℋ;

(iii) if ƒ and g are in ℋ and g is non-zero for all sufficiently large values of x, then

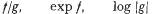
are also in ℋ.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 1 , Issue 4 , December 1960 , pp. 396 - 418
Copyright
Copyright © Australian Mathematical Society 1960

References

[1] Bourbaki, N., Éléments de Mathématique, Book 4, Chapter 5 (Paris, 1951), Appendix.Google Scholar
[2] du Bois-Reymond, P., Sur la grandeur relative des infinis des fonctions, Annali di Matematica, (2), 4 (1871), 338–353.CrossRefGoogle Scholar
[3] du Bois-Reymond, P., Théorème général concernant la grandeur relative des infinis des fonctions et de leurs derivées, Jour. für Mathematik, 74 (1872), 294–304.Google Scholar
[4] Hadamard, J., Sur les charactéres de convergence des séries à termes positifs et sur les fonctions indéfiniment croissantes, Acta Mathematica, 18 (1894), 319–336.CrossRefGoogle Scholar
[5] Hardy, G. H., Pure Mathematics, 1st Edn., Cambridge (1908).Google Scholar
[6] Hardy, G. H., Orders of Infinity, Cambridge Tracts in Mathematics, No. 12, Cambridge (1910).Google Scholar
[7] Rogers, C. A. and Taylor, S. J., Additive set functions in Euclidean space, Acta Mathematica, 101 (1959) 273–302.CrossRefGoogle Scholar