Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T12:19:23.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Saddle point theorem and nonlinear scalar Neumann boundary value problems

Part of: Boundary value problems

Published online by Cambridge University Press:  09 April 2009

M. N. Nkashama
M. N. Nkashama
Affiliation:
University of Alabama at BirminghamBiringham, Alabama 35294, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are concerned with existence results for nonlinear scalar Neumann boundary value problems u″ + g(x, u) = 0, u′(0) = u′(π) = 0 where g(x, u) satisfies Carathéodory conditions and is (possibly) unbounded. On the one hand we only assume that the function (sgn u)g(x, u) is bounded either from above or from below in some function space, and we impose conditions which relate the asymptotic behavior of the function (for¦u¦large) with the first two eigenvalues of the corresponding linear problem (here G(x, u) = 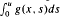is the potential generated by g). On the other hand we consider cases where the function (sgn u)g(x, u) is unbounded. The potential G(x, u) is not necessarily required to satisfy a convexity condition. Our method of proof is variational, we make use of the Saddle Point Theorem.

MSC classification

Secondary: 34B15: Nonlinear boundary value problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 55 , Issue 3 , December 1993 , pp. 386 - 402
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Ahmad, S. and Lazer, A. C., ‘Critical point theory and a theorem of Amaral and Pera’, Boll. Un. Mat. Ital. B3 (1984), 583–598.Google Scholar
[2]Ahmad, S., Lazer, A. C. and Paul, J. L., ‘Elementary critical point theory and perturbation of elliptic boundary value problems at resonance’, Indiana University Math. J. 25 (1976), 933–944.CrossRefGoogle Scholar
[3]Brézis, H., Analyse fonctionnelle: Théorie et applications, 2e tirage (Masson, Paris, 1987).Google Scholar
[4]de Figueiredo, D. G. and Gossez, J. P., ‘Nonresonance below the first eigenvalue for a semilinear elliptic problem’, Math. Ann. 281 (1988), 589–610.CrossRefGoogle Scholar
[5]Fonda, A. and Gossez, J. P., ‘Semicoercive variational problems at resonance: An abstract approach’, preprint, 1988.Google Scholar
[6]Fonda, A. and Lupo, D., ‘Periodic solutions of second order ordinary differential equations’, Séminaire mathématique (nouvelle série), (Université de Louvain, Rapport n° 127, Mars 1988).Google Scholar
[7]Hammerstein, A., ‘Nichtlineare Integralgleichugen nebst Anwendugen’, Acta Math. 54 (1930), 117–176.CrossRefGoogle Scholar
[8]Iannacci, R. and Nkashama, M. N., ‘Unbounded perturbations of forced second order ordinary differential equations at resonance’, J. Differential Equations 69 (1987), 289–309.CrossRefGoogle Scholar
[9]Mawhin, J. and Ward, J. R. Jr, ‘Periodic solutions of some forced liénard differential equations at resonance’, Arch. Math. (Basel) 41 (1983), 337–351.CrossRefGoogle Scholar
[10]Mawhin, J., Ward, J. R. Jr and Willem, M., ‘Variational methods and semi-linear elliptic equations’, Arch. Rational Mech. Anal. 95 (1986), 269–277.CrossRefGoogle Scholar
[11]Rabinowitz, P. H., Minimax methods in critical point theory with applications to differential equations, CBMS Regional Conf. Ser. in Math., 65 (American Math. Soc., Providence, 1986).CrossRefGoogle Scholar
[12]Ramos, M. and Sanchez, L., ‘Variational elliptic problems involving noncoercive functionals’, Proc. Royal Soc. Edinburgh Sect. A 112 (1989), 177–185.CrossRefGoogle Scholar