Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watbled, Fr�d�rique
1996.
Rosenthal sets for Banach-valued functions.
Archiv der Mathematik,
Vol. 66,
Issue. 6,
p.
479.


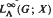 is separable then
is separable then 