Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-02T20:59:43.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings related to completely 0-simple semigroups

Published online by Cambridge University Press:  09 April 2009

D. B. McAlister
D. B. McAlister
Affiliation:
Department of Pure Mathematics Queen's University, Belfast
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A.H. Clifford ([2], [3]) has shown that all finite dimensional irreducible representations of a completely 0-simple semigroup can be obtained as extensions of those of its maximal subgroups. Lallement and Petrich, [7], have given an alternative method for constructing the irreducible representations of a finite 0-simple semigroup from its Schutzenberger representation ([13]). Using the form which they obtain for the irreducible representations of a finite 0-simple semigroup S = M0(G; m, n; P), Lallement and Petrich show that 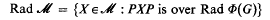where M is the Munn algebra isomorphic to the (contracted) algebra Φ(S) of S over Φ.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 12 , Issue 3 , August 1971 , pp. 257 - 274
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Brown, W. P., ‘Generalised matrix algebras’, Canadian J. Math. 7 (1955), 188–190.CrossRefGoogle Scholar
[2]Clifford, A. H., ‘Matrix representations of completely simple semigroups’, Amer. J. Math. 64 (1942), 327–342.CrossRefGoogle Scholar
[3]Clifford, A. H., ‘Basic representations of completely simple semigroups’, Amer. J. Math. 82 (1960), 430–434.CrossRefGoogle Scholar
[4]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1 (Math. Survey 7, Amer. Math. Soc., 1961)Google Scholar
[5]Green, J. A., ‘On the structure of semigroups’, Annals of Math. 54 (1951), 163–172.CrossRefGoogle Scholar
[6]Jacobson, N., The Structure of rings (American Math. Soc. Colloquium Publications, Vol. 37, 1956).Google Scholar
[7]Lallement, G. and Petrich, M., ‘Irreducible matrix representations of finite semigroups’, Trans. Amer. Math. Soc. 139 (1969), 393–412.CrossRefGoogle Scholar
[8]McAlister, D. B., ‘Basic representations of arbitrary semigroups’, Trans. Amer. Math. Soc. 135 (1969), 311–342.CrossRefGoogle Scholar
[9]McAlister, D. B., ‘The category of representations of a completely 0-simple semigroup’, J. Austr. Math. Soc. 2 (1971), 193–210.CrossRefGoogle Scholar
[10]McCoy, N. H., The theory of rings (Macmillan, New York, 1964).Google Scholar
[11]Munn, W. D., ‘On semigroup algebras’, Proc. Camb. Phil. Soc. 51 (1955), 1–15.CrossRefGoogle Scholar
[12]Munn, W. D., ‘Irreducible matrix representations of semigroups’, Quarterly Jour. Math. Oxford, Ser. (2), 11 (1960), 295–309.CrossRefGoogle Scholar
[13]Schutzenberger, M. P., ‘D représentation des demigroupes’, C. R. Acad. Sci. Paris. 224 (1957) 1994–96.Google Scholar
[14]Theirrin, G., ‘Demigroupes inversés et rectangulaires’, Bull. Roy. Belg. Bull. Cl. Sci. (5), 41 (1955), 83–92.Google Scholar