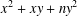Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T09:22:02.124Z Has data issue: false hasContentIssue false
  • English
  • Français

REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM $x^{2}+xy+ny^{2}$

Part of: Multiplicative number theory Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  17 November 2015

BUMKYU CHO
BUMKYU CHO*
Affiliation:
Department of Mathematics, Dongguk University-Seoul, 30 Pildong-ro 1-gil, Jung-gu, Seoul100-715, Republic of Korea email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In terms of class field theory we give a necessary and sufficient condition for an integer to be representable by the quadratic form 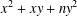$x^{2}+xy+ny^{2}$ (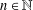$n\in \mathbb{N}$ arbitrary) under extra conditions 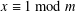$x\equiv 1\;\text{mod}\;m$, 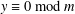$y\equiv 0\;\text{mod}\;m$ on the variables. We also give some examples where their extended ring class numbers are less than or equal to 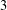$3$.

Keywords

quadratic formsclass field theory

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Secondary: 11R37: Class field theory 11F11: Holomorphic modular forms of integral weight
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 182 - 191
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Chen, I. and Yui, N., ‘Singular values of Thompson series’, in: Groups, Difference Sets, and The Monster (Columbus, OH, 1993), Ohio State University Mathematical Research Institute Publications, 4 (eds. Arasu, K. T., Dillon, J. F., Harada, K., Sehgal, S. and Solomon, R.) (de Gruyter, Berlin, 1996), 255–326.CrossRefGoogle Scholar
Cho, B., ‘Primes of the form x 2 + ny 2 with conditions x ≡ 1 mod N, y ≡ 0 mod N’, J. Number Theory 130 (2010), 852–861.CrossRefGoogle Scholar
Cho, B., ‘Integers of the form x 2 + ny 2’, Monatsh. Math. 174 (2014), 195–204.Google Scholar
Cho, B. and Koo, J. K., ‘Construction of class fields over imaginary quadratic fields and applications’, Q. J. Math. 61 (2010), 199–216.Google Scholar
Cox, D., Primes of the Form x 2 + ny 2, 2nd edn (Wiley, Hoboken, NJ, 2013).Google Scholar
Dickson, L. E., History of the Theory of Numbers, Volume III: Quadratic and Higher Forms (Dover Publications, New York, 2005).Google Scholar
Eum, I. S., Koo, J. K. and Shin, D. H., ‘Primitive generators of certain class fields’, J. Number Theory 155 (2015), 46–62.Google Scholar
Gee, A., ‘Class invariants by Shimura’s reciprocity law’, J. Théor. Nombres Bordeaux 11 (1999), 45–72.Google Scholar
Gurak, S., ‘On the representation theory for full decomposable forms’, J. Number Theory 13 (1981), 421–442.Google Scholar
Hasse, H., ‘Über den Klassenkörper zum quadratischen Zahlkörper mit der Diskriminante −47’, Acta Arith. 9 (1964), 419–434.CrossRefGoogle Scholar
Stevenhagen, P., ‘Hilbert’s 12th problem, complex multiplication, and Shimura reciprocity’, in: Class Field Theory—Its Centenary and Prospect, Advanced Studies in Pure Mathematics, 30 (ed. Miyake, K.) (Mathematical Society of Japan, Tokyo, 2001), 161–176.Google Scholar
Williams, K. S. and Hudson, R. H., ‘Representation of primes by the principal form of discriminant − D when the classnumber h (−D) is 3’, Acta Arith. 57 (1991), 131–153.Google Scholar