Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T09:15:25.789Z Has data issue: false hasContentIssue false
  • English
  • Français

REPRESENTATION THEOREMS FOR NORMED ALGEBRAS

Part of: Topological algebras, normed rings and algebras, Banach algebras Fairly general properties Commutative Banach algebras and commutative topological algebras Rings and algebras arising under various constructions Linear function spaces and their duals

Published online by Cambridge University Press:  17 June 2013

M. R. KOUSHESH
M. R. KOUSHESH*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156–83111, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box: 19395–5746, Tehran, Iran
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that for a normal locally-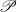$\mathscr{P}$ space 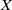$X$ (where 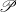$\mathscr{P}$ is a topological property subject to some mild requirements) the subset 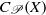${C}_{\mathscr{P}} (X)$ of 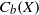${C}_{b} (X)$ consisting of those elements whose support has a neighborhood with 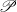$\mathscr{P}$, is a subalgebra of 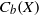${C}_{b} (X)$ isometrically isomorphic to 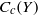${C}_{c} (Y)$ for some unique (up to homeomorphism) locally compact Hausdorff space 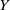$Y$. The space 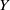$Y$ is explicitly constructed as a subspace of the Stone–Čech compactification 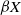$\beta X$ of 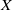$X$ and contains 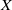$X$ as a dense subspace. Under certain conditions, 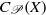${C}_{\mathscr{P}} (X)$ coincides with the set of those elements of 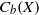${C}_{b} (X)$ whose support has 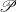$\mathscr{P}$, it moreover becomes a Banach algebra, and simultaneously, 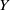$Y$ satisfies 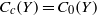${C}_{c} (Y)= {C}_{0} (Y)$. This includes the cases when 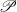$\mathscr{P}$ is the Lindelöf property and 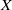$X$ is either a locally compact paracompact space or a locally-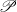$\mathscr{P}$ metrizable space. In either of the latter cases, if 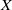$X$ is non-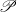$\mathscr{P}$, then 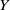$Y$ is nonnormal and 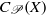${C}_{\mathscr{P}} (X)$ fits properly between 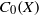${C}_{0} (X)$ and 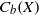${C}_{b} (X)$; even more, we can fit a chain of ideals of certain length between 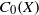${C}_{0} (X)$ and 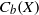${C}_{b} (X)$. The known construction of 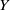$Y$ enables us to derive a few further properties of either 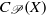${C}_{\mathscr{P}} (X)$ or 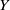$Y$. Specifically, when 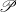$\mathscr{P}$ is the Lindelöf property and 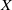$X$ is a locally-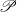$\mathscr{P}$ metrizable space, we show that

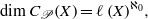$$\begin{eqnarray*}\dim C_{\mathscr{P}}(X)= \ell \mathop{(X)}\nolimits ^{{\aleph }_{0} } ,\end{eqnarray*}$$
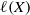where $\ell (X)$ is the Lindelöf number of 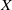$X$, and when 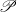$\mathscr{P}$ is countable compactness and 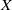$X$ is a normal space, we show that
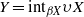$$\begin{eqnarray*}Y= {\mathrm{int} }_{\beta X} \upsilon X\end{eqnarray*}$$
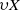 where $\upsilon X$ is the Hewitt realcompactification of 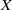$X$.

Keywords

Stone–Čech compactificationcommutative Gelfand–Naimark theoremreal Banach algebraGelfand theorycompact supportLindelöfHewitt realcompactificationcountably compact

MSC classification

Secondary: 46J10: Banach algebras of continuous functions, function algebras 46J25: Representations of commutative topological algebras 46E25: Rings and algebras of continuous, differentiable or analytic functions 46E15: Banach spaces of continuous, differentiable or analytic functions 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.) 46H05: General theory of topological algebras 16S60: Rings of functions, subdirect products, sheaves of rings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 2 , October 2013 , pp. 201 - 222
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Acharyya, S. K. and Ghosh, S. K., ‘Functions in $C(X)$ with support lying on a class of subsets of $X$’, Topology Proc. 35 (2010), 127–148.Google Scholar
Acharyya, S. K., Chattopadhyay, K. C. and Ghosh, P. P., ‘The rings ${C}_{K} (X)$ and ${C}_{\infty } (X)$—some remarks’, Kyungpook Math. J. 43 (2003), 363–369.Google Scholar
Afrooz, S. and Namdari, M., ‘${C}_{\infty } (X)$ and related ideals’, Real Anal. Exchange 36 (2010), 45–54.CrossRefGoogle Scholar
Aliabad, A. R., Azarpanah, F. and Namdari, M., ‘Rings of continuous functions vanishing at infinity’, Comment. Math. Univ. Carolin. 45 (2004), 519–533.Google Scholar
Behrends, E., M-structure and the Banach–Stone Theorem (Springer, Berlin, 1979).CrossRefGoogle Scholar
Burke, D. K., ‘Covering properties’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 347–422.CrossRefGoogle Scholar
Comfort, W. W., ‘On the Hewitt realcompactification of a product space’, Trans. Amer. Math. Soc. 131 (1968), 107–118.CrossRefGoogle Scholar
Engelking, R., General Topology, 2nd edn (Heldermann, Berlin, 1989).Google Scholar
Hager, A. W. and Johnson, D. G., ‘A note on certain subalgebras of $C(X)$’, Canad. J. Math. 20 (1968), 389–393.CrossRefGoogle Scholar
Gillman, L. and Jerison, M., Rings of Continuous Functions (Springer, New York, 1976).Google Scholar
Good, C., ‘The Lindelöf property’, in: Encyclopedia of General Topology (eds. Hart, K. P., Nagata, J. and Vaughan, J. E.) (Elsevier, Amsterdam, 2004), 182–184.Google Scholar
Hodel, R. E. Jr, ‘Cardinal functions I’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 1–61.Google Scholar
Koushesh, M. R., ‘Compactification-like extensions’, Dissertationes Math. (Rozprawy Mat.) 476 (2011), 88 pp.Google Scholar
Koushesh, M. R., ‘The partially ordered set of one-point extensions’, Topology Appl. 158 (2011), 509–532.CrossRefGoogle Scholar
Koushesh, M. R., ‘A pseudocompactification’, Topology Appl. 158 (2011), 2191–2197.CrossRefGoogle Scholar
Koushesh, M. R., ‘The Banach algebra of continuous bounded functions with separable support’, Studia Math. 210 (2012), 227–237.CrossRefGoogle Scholar
Koushesh, M. R., ‘Connectedness modulo a topological property’, Topology Appl. 159 (2012), 3417–3425.CrossRefGoogle Scholar
Koushesh, M. R., ‘Topological extensions with compact remainder’, J. Math. Soc. Japan, in press.Google Scholar
Koushesh, M. R., ‘Representation theorems for Banach algebras’ (submitted) arXiv:1302.2039.Google Scholar
Koushesh, M. R., ‘Continuous mappings with null support’. Topology Appl., to appear, arXiv:1302.2235.Google Scholar
Porter, J. R. and Woods, R. G., Extensions and Absolutes of Hausdorff Spaces (Springer, New York, 1988).CrossRefGoogle Scholar
Stephenson, R. M. Jr, ‘Initially $\kappa $-compact and related spaces’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 603–632.CrossRefGoogle Scholar
Taherifar, A., ‘Some generalizations and unifications of ${C}_{K} (X), {C}_{\psi } (X)$ and ${C}_{\infty } (X)$. arXiv:1210.6521.Google Scholar
Vaughan, J. E., ‘Countably compact and sequentially compact spaces’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 569–602.CrossRefGoogle Scholar
Warren, N. M., ‘Properties of Stone–Čech compactifications of discrete spaces’, Proc. Amer. Math. Soc. 33 (1972), 599–606.Google Scholar
Weir, M. D., Hewitt–Nachbin Spaces (American Elsevier, New York, 1975).Google Scholar