Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T08:47:53.598Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS

Part of: Graph theory Permutation groups Algebraic combinatorics

Published online by Cambridge University Press:  20 November 2015

CAI HENG LI  and
LEI WANG
CAI HENG LI
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunming, Yunnan 650091, PR China School of Mathematics and Statistics, The University of Western Australia, Crawley, WA 6009, Australia email [email protected]
LEI WANG*
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunming, Yunnan 650091, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a problem of characterising a family of Cayley graphs, we study a class of finite groups 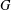$G$ which behave similarly to elementary abelian 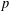$p$-groups with 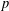$p$ prime, that is, there exists a subgroup 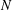$N$ such that all elements of $G\setminus N$ are conjugate or inverse-conjugate under 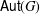$\mathsf{Aut}(G)$. It is shown that such groups correspond to complete multipartite graphs which are normal edge-transitive Cayley graphs.

Keywords

Cayley graphcomplete graphREA groupFrobenius group

MSC classification

Primary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 05E18: Group actions on combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 241 - 251
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Biggs, N., Algebraic Graph Theory (Cambridge University Press, Cambridge, 1993).Google Scholar
Camina, A. R., ‘Some conditions which almost characterize Frobenius groups’, Israel J. Math. 31 (1978), 153–160.CrossRefGoogle Scholar
Dark, R. and Scoppola, C. M., ‘On Camina groups of prime power order’, J. Algebra 181 (1996), 787–802.Google Scholar
Devillers, A., Giudici, M., Li, C. H., Pearce, G. and Praeger, C. E., ‘On imprimitive rank 3 permutation groups’, J. Lond. Math. Soc. (2) 84 (2011), 649–669.Google Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘On normal 2-geodesic transitive Cayley graphs’, J. Algebraic Combin. 39 (2014), 903–918.Google Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, Hong Kong, New York, 1996).Google Scholar
Fan, W. W., Leemans, D., Li, C. H. and Pan, J. M., ‘Locally 2-arc-transitive complete bipartite graphs’, J. Combin. Theory Ser. A 120 (2013), 683–699.CrossRefGoogle Scholar
Fan, W. W., Li, C. H. and Pan, J. M., ‘Finite locally-primitive complete bipartite graphs’, J. Group Theory 17 (2014), 111–129.Google Scholar
Godsil, C. D., ‘On the full automorphism group of a graph’, Combinatorica 1 (1981), 243–256.Google Scholar
Lewis, M. L., ‘Generalizing Camina groups and their character tables’, J. Group Theory 12 (2009), 209–218.Google Scholar
Lewis, M. L., ‘On p-group Camina pairs’, J. Group Theory 15 (2012), 469–483.Google Scholar
Li, C. H. and Qiao, S. H., ‘Finite groups of fourth-power free order’, J. Group Theory 16 (2013), 275–298.Google Scholar
Mlaiki, N. M., ‘Camina triples’, Canad. Math. Bull. 57 (2014), 125–131.Google Scholar
Praeger, C. E., ‘Finite normal edge-transitive Cayley graphs’, Bull. Aust. Math. Soc. 60 (1999), 207–220.Google Scholar
Xu, M. Y., ‘Automorphism groups and isomorphisms of Cayley digraphs’, Discrete Math. 182 (1998), 309–319.Google Scholar