Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T07:03:33.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative amenability and the non-amenability of B(l1)

Part of: General commutative ring theory Integral domains Commutative Banach algebras and commutative topological algebras Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  09 April 2009

C. J. Read
C. J. Read
Affiliation:
Faculty of Mathematics, University of Leeds, Leeds LS2 9JT, United Kingdom, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we begin with a short, direct proof that the Banach algebra B(l1) is not amenable. We continue by showing that various direct sums of matrix algebras are not amenable either, for example the direct sum of the finite dimensional algebras 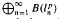is no amenable for 1 ≤ p ≤ ∞, p ≠ 2. Our method of proof naturally involves free group algebras, (by which we mean certain subalgebras of B(X) for some space X with symmetric basis—not necessarily X = l2) and we introduce the notion of ‘relative amenability’ of these algebras.

Keywords

amenableBanach algebraoperator algebra.

MSC classification

Secondary: 46J20: Ideals, maximal ideals, boundaries 46H10: Ideals and subalgebras 46H20: Structure, classification of topological algebras 13A05: Divisibility; factorizations 13G05: Integral domains 46J05: General theory of commutative topological algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 80 , Issue 3 , June 2006 , pp. 317 - 333
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Bollobsá, B.Random graphs (Academic Press, London, 1985).Google Scholar
[2]Connes, A. ‘Classification of injective factors’, Ann. of Math. (2) 104 (1976), 73–115.CrossRefGoogle Scholar
[3]Dales, H. G., Banach algebras and automatic continuity, London Mathematical Society Monographs, New Series 24 (Oxford University Press, New York, 2001).Google Scholar
[4]Haagerup, U. ‘All nuclear C*-algebras are amenable’, Invent. Math. 74 (1983), 93–116.CrossRefGoogle Scholar
[5]Ozawa, N. ‘A note on non-amenability of B(lp) for p = 1, 2’, Internat. J. Math. 15 (2004), 557–565.Google Scholar
[6]Pisier, G. ‘On Read's proof that B(l1) is not amenable’, in: Geometric aspects of functional analysis, Lecture Notes in Math. 1850 (Springer, Berlin, 2004).Google Scholar