REGULARITY OF AML FUNCTIONS IN TWO-DIMENSIONAL NORMED SPACES

Abstract

Savin [‘ 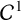$\mathcal {C}^{1}$ regularity for infinity harmonic functions in two dimensions’, Arch. Ration. Mech. Anal. 3(176) (2005), 351–361] proved that every planar absolutely minimizing Lipschitz (AML) function is continuously differentiable whenever the ambient space is Euclidean. More recently, Peng et al. [‘Regularity of absolute minimizers for continuous convex Hamiltonians’, J. Differential Equations 274 (2021), 1115–1164] proved that this property remains true for planar AML functions for certain convex Hamiltonians, using some Euclidean techniques. Their result can be applied to AML functions defined in two-dimensional normed spaces with differentiable norm. In this work we develop a purely non-Euclidean technique to obtain the regularity of planar AML functions in two-dimensional normed spaces with differentiable norm.

1 Introduction

Let $n\geq 2$ and $\Omega \subset \mathbb {R}^{n}$ be a nonempty open and connected set, where $\mathbb {R}^{n}$ is equipped with the Euclidean norm. Aronsson in [1] studied the class of $\mathcal {C}^{2}$ -smooth infinite-harmonic functions defined on $\Omega $ , that is, classical solutions of the equation given by the infinity-Laplacian,

(1-1) $$ \begin{align} \Delta_{\infty} u:= \sum_{i,j=1}^{n}u_{x_{i}}u_{x_{j}}u_{x_{i}x_{j}}=0. \end{align} $$

This equation arises from considering the following optimal Lipschitz extension problem. Let $g:\partial \Omega \to \mathbb {R}$ be a continuous function. Find a function $u:\overline {\Omega }\to \mathbb {R}$ such that $g=u|_{\partial \Omega }$ and that, for every open set V compactly contained in $\Omega $ and for every function $h:\overline {V}\to \mathbb {R}$ such that $u|_{\partial V}=h|_{\partial V}$ , the following estimate holds:

$$ \begin{align*}\mathrm{Lip}(u|_{V})\leq \mathrm{Lip}(h|_{V}).\end{align*} $$

The above problem leads to the following definition.

Definition 1.1. Let $(X,\|\cdot \|)$ be a finite-dimensional Banach space and let $\Omega $ be an open subset of X. We say that a locally Lipschitz function $u:\Omega \subset X\to \mathbb {R}$ is a $\|\cdot \|$ -absolute minimizing Lipschitz function ( $\|\cdot \|$ -AML function), if for every open set V compactly contained in $\Omega $ and for every function $g:\overline {V}\to \mathbb {R}$ such that $u|_{\partial V}=g|_{\partial V}$ , the following estimate holds:

$$ \begin{align*}\mathrm{Lip}(u|_{V})\leq \mathrm{Lip}(g|_{V}).\end{align*} $$

If no confusion arises from the underlying norm on X, we just write ‘AML function’.

Let us now present some results in the Euclidean setting. Aronsson showed that $\mathcal {C}^{2}$ -smooth infinity-harmonic functions coincide with $\mathcal {C}^{2}$ -smooth AML functions. In [9], Jensen proved that solutions of Equation (1-1) in the viscosity sense coincide with AML functions. Further, Jensen proved the existence and uniqueness of a viscosity solution of Equation (1-1) satisfying a given continuous boundary condition. Further information about the existence and uniqueness of solutions of the equation governed by the infinity-Laplacian operator can be found in [2]. A link between this theory and the stochastic tug-of-war game theory is presented in [11].

The regularity of AML functions is one of the main issues in this field. In the seminal paper [12] it is proven that planar $\|\cdot \|_{2}$ -AML functions are continuously differentiable, where $\|\cdot \|_{2}$ is a Euclidean norm. In [6] it is shown that each planar $\|\cdot \|_{2}$ -AML function is $\mathcal {C}^{1,\alpha }$ -smooth for some $\alpha>0$ . Also, provided with tools from capacity theory, in [13] we can find an alternative proof of the smoothness of planar $\|\cdot \|_{2}$ -AML functions. Further results assert that AML functions in (finite-dimensional) Euclidean spaces are at least everywhere differentiable; see [7, 8]. However, the continuity of the differential remains an open question in higher dimensions.

The main question we address here is as follows.

Question 1.2. If $(X,\|\cdot \|)$ is a finite-dimensional normed space, which property of the norm guarantees the smoothness of all $\|\cdot \|$ -AML functions defined on open subsets of X?

In [10] we can find a different approach which encompasses Question 1.2. In that paper, $(X,\|\cdot \|)$ is considered as an n-dimensional Euclidean space and a Hamiltonian formulation of the AML property is given. More precisely, let $H:X\to \mathbb {R}$ be a coercive, convex function. A locally Lipschitz function $u:\Omega \subset X\to \mathbb {R}$ is said to be an $\text{AML}_{H}$ function if for every open set V compactly contained in $\Omega $ and every absolutely continuous function $g:\overline {V}\to \mathbb {R}$ such that $u|_{\partial V}=g|_{\partial V}$ , the following estimate holds:

$$ \begin{align*} \text{ess}\sup (H(u^{\prime}|_{V}))\leq \text{ess}\sup(H(g^{\prime}|_{V})),\end{align*} $$

where this notion is well defined thanks to Rademacher’s theorem, which asserts that Lipschitz functions in finite-dimensional spaces are differentiable almost everywhere.

In this notation, Question 1.2 is reinterpreted as follows. Let H be a norm on $\mathbb {R}^{n}$ . Then $u:\Omega \subset \mathbb {R}^{n}\to \mathbb {R}$ is an $\text{AML}_{H}$ function if and only if u is an $\|\cdot \|$ - $\text{AML}$ function such that H can be seen as the canonical dual norm of $(\mathbb {R}^{n},\|\cdot \|)$ .

To state the main results of [10], we need the following notation. Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function and $x\in \Omega $ . For $r\in (0, \mathrm {dist}(x,\partial \Omega ))$ , we set

$$ \begin{align*}S(x,r)^{+}=S_{u}(x,r)^{+}:= \max_{\|y-x\|=r} \frac{u(y)-u(x)}{r}.\end{align*} $$

By Corollary 2.3,

$$ \begin{align*}S(x)=S_{u}(x):= \lim_{r\to 0} S(x,r)^{+}\text{ exists} \quad \text{and}\quad 0\leq S(x)\leq S^{+}(x,r).\end{align*} $$

So, the results of [10] applied to the case when H is a norm are stated in Theorems 1.3 and 1.4.

Theorem 1.3 [10, Theorem 1.1]

Let X be a finite-dimensional Banach space with differentiable norm and let $\Omega $ be an open subset of X. Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function. Then for each $x\in \Omega $ and $0<r<\mathrm {dist}(x,\partial \Omega )$ , there exists a vector $e_{x,r}^{*}\in X^{*}$ , with $\|e_{x,r}^{*}\|=S(x)$ , such that

$$ \begin{align*}\max_{y\in B_{r}(x)}\dfrac{|u(y)-u(x)-e^{*}_{x,r}(y-x)|}{r}\rightarrow 0 \quad\text{as }r\rightarrow 0.\end{align*} $$

Observe that, thanks to Theorem 1.3, in order to prove that an $\|\cdot \|$ -AML function is differentiable at some $x\in \Omega $ , it is enough to prove that the net $(e_{x,r}^{*})_{r}$ converges as r tends to $0$ . A nice example given by D. Preiss (mentioned in [4, 10]) shows that there is a Lipschitz function from $\mathbb {R}$ to $\mathbb {R}$ which is nondifferentiable at $0$ for which we can find a net of linear maps $(e_{0,r}^{*})_{r}$ satisfying the conclusion of Theorem 1.3. However, the convergence of the mentioned net and the continuity of the differential are guaranteed by the following theorem.

Theorem 1.4 [10, Theorem 1.2]

Let X be a two-dimensional Banach space. The following statements are equivalent.

1. (a) The underlying norm is differentiable in $X\setminus \{0\}$ .

2. (b) Every AML function defined on an open subset of X is continuously differentiable.

3. (c) Every AML function defined on an open subset of X is everywhere differentiable.

Even though the results of [10] can be applied to general finite-dimensional normed spaces, the technique used to obtain these theorems relies on the Euclidean structure of the ambient space.

The main contribution of this work is to provide a purely non-Euclidean technique to prove Theorem 1.4. Moreover, for the sake of completeness, we present a proof of Theorem 1.3 in a purely non-Euclidean fashion as well. A notable difference between our approach and the one presented in [10] it is the fact that the latter avoids dealing with positively homogeneous convex functions (see [10, point (2) in Section 1.1]), while we work directly with them.

Our main result is Theorem 1.4. Its proof relies on Theorem 1.3 and the following result.

Theorem 1.5. Let X be a two-dimensional normed space with differentiable norm. There exists a function ${\delta :(0,\infty )\to (0,\infty )}$ satisfying the following property. Given an AML function $u:\text {int}(B_{1})\subset X\to \mathbb {R}$ such that $S(0)\ne 0$ and $\varepsilon>0$ , if there exists $e_{1}^{*}\in X^{*}$ such that

$$ \begin{align*}\sup_{x\in \text{int}(B_{1})}|u(x)-e_{1}^{*}(x)|\leq \delta(\varepsilon)\|e_{1}^{*}\|, \end{align*} $$

then $\displaystyle \limsup _{r\to 0}\|e_{0,r}^{*}-e_{1}^{*}\|\leq \varepsilon \|e_{1}^{*}\|$ .

Proof of Theorem 1.4

The implication from (b) to (c) is trivial and the implication from (c) to (a) is given by Corollary 2.8, which asserts that the underlying norm of X, restricted to $X\setminus \{0\}$ , is an AML function. So, we only have to prove that (a) implies (b). From now on, we denote by $B_{r}$ the closed ball of radius r centered at the origin.

Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function. Let $x_{0}\in \Omega $ . Let us first prove that u is differentiable at $x_{0}$ . Since we are only interested in the differentiability of u, replacing if necessary u by $Ru({\cdot -x_{0}}/{R})-u(x_{0})$ for some $R>0$ , we can assume that $x_{0}=0$ , $u(0)=0$ and $B_{1}\subset \Omega $ . By Theorem 1.3, there exists $(e^{*}_{r})_{r}\subset X^{*}$ such that $\|e^{*}_{r}\|=S(0)$ for every $r\in (0,1)$ and

$$ \begin{align*}|u(x)-e_{r}^{*}(x)|\leq r\sigma(r),\quad\text{for all }x\in B_{r},\end{align*} $$

where $\sigma :\mathbb {R}_{+}\to \mathbb {R}$ is a positive function such that $\sigma (r)$ tends to $0$ as r tends to $0$ . If $S(0)=0$ , then $e^{*}_{r}=0$ for all $r>0$ , so u is differentiable at $0$ , $u^{\prime }(0)=0$ and $\|u^{\prime }(0)\|=S(0)$ . We now assume $S(0)>0$ . Let us prove that $e_{r}^{*}$ converges as r tends to $0$ . Let $\varepsilon>0$ . We fix $s=s(\varepsilon )$ such that $\sigma (s)\leq \delta (\varepsilon )S(0)$ . The function $v:=({1}/{s})u(s\cdot )$ is well defined on $B_{1}$ and, for all $x\in B_{1}$ , we have $\vert v(x)-e_{s}^{*}(x)\vert \le \delta (\varepsilon )\|e_{s}^{*}\|$ . According to Theorem 1.5 applied to the function v, we get

$$ \begin{align*}\limsup_{r\to 0}\|e_{r}^{*}-e_{s}^{*}\| \leq\varepsilon \|e_{s}^{*}\|.\end{align*} $$

If $\ell $ is any accumulation point of $(e_{s(\varepsilon )}^{*})_{\varepsilon }$ , the above inequality implies that for every $\varepsilon>0$ ,

$$ \begin{align*}\limsup_{r\to 0}\|e_{r}^{*}-\ell\| \leq\varepsilon S(0).\end{align*} $$

We have proved that $(e_{r}^{*})_{r}$ converges to $\ell $ . Therefore, u is differentiable at $0$ and $u^{\prime }(0)=\ell $ . Moreover, since $\|e_{r}^{*}\|=S(0)$ for all r, we have that $\|u^{\prime }(0)\|=S(0)$ . Using Theorem 1.5 again, we make the following claim.

Claim. If u is any AML function defined on $B_{1}$ such that $S(0)>0$ , $e_{1}^{*}$ is a nonzero linear form and $\vert u(x)-e_{1}^{*}(x)\vert \le \delta (\varepsilon )\|e_{1}^{*}\|$ on $B_{1}$ , then $\|u^{\prime }(0)-e_{1}^{*}\|=\lim _{r\to 0}\|e_{r}^{*}-e_{1}^{*}\| \le \varepsilon $ .

Let us now check the continuity of $u^{\prime }$ . If $S(0)>0$ , fix $\varepsilon>0$ and denote $\delta =\delta (\varepsilon )$ . Let $0<r_{0}<\mathrm {dist}(0,\partial \Omega )$ be such that, for all $r\le r_{0}$ , $\sigma (r)\le \delta (\varepsilon )S(0)/2$ . Fix $r<r_{0}$ . The function $v(\cdot )= u(r\cdot )/r$ restricted to $B_{1}$ satisfies

$$ \begin{align*}|v(x) -e^{*}_{r}(x)|\leq \dfrac{\delta}{2} S(0)= \dfrac{\delta}{2}\|e^{*}_{r}\|\quad \text{for all }x\in B_{1}.\end{align*} $$

By the above claim, we obtain that $\|u^{\prime }(0)-e_{r}^{*}\|\leq \varepsilon \|e^{*}_{r}\|$ . Let $y\in B_{r/2}$ . If ${w:B_{1}\to \mathbb {R}}$ is defined by $w(\cdot ):=({2}/{r})(u({r}/{2}\cdot +y)-e^{*}_{r}(y))$ , we have $\vert w(x)-e_{r}^{*}(x)\vert \leq \delta \| e_{r}^{*}\|$ on  $B_{1}$ . The above claim shows that $\|w^{\prime }(0)-e_{r}^{*}\|=\|u^{\prime }(y)-e_{r}^{*}\|\leq \varepsilon \|e^{*}_{r}\|$ , and hence, that ${\|u^{\prime }(0)-u^{\prime }(y)\|\leq 2\varepsilon S(0)}$ . This proves the continuity of $u^{\prime }$ at $0$ .

Let us prove the continuity of $u^{\prime }$ in the case $S(0)=0$ . Let us fix $\varepsilon>0$ . By definition of $S(0)$ , there exists $0<r< \mathrm {dist}(0,\partial \Omega )$ such that $S(0,r)^{+}<\varepsilon $ . By the continuity of $S(\cdot ,r)^{+}$ , $S(x,r)^{+}<\varepsilon $ in a neighborhood W of $0$ . Finally, $\|u^{\prime }(x)\|= S(x)\leq S(x,r)^{+}<\varepsilon $ for all $x\in W$ .□

Furthermore, as a consequence of Theorem 1.5 we obtain the following two corollaries. The proofs of these results follow without any significant change from the proofs for Euclidean spaces X presented in [12, Theorems 3 and 4]. Corollary 1.7 is also stated in [10, Theorem 1.2(D)] in the more general framework of $\text{AML}_{H}$ functions.

Corollary 1.6 [12, Theorem 3]

Let X be a two-dimensional normed space with differentiable norm. There exists a function $\rho :[0,1]\to \mathbb {R}$ , satisfying $\lim _{t\to 0}\rho (t)=0$ , such that for any AML function $u:\text {int}(B_{1}) \to \mathbb {R}$ , with $\mathrm {Lip}(u)\leq 1$ , the following inequality holds:

$$ \begin{align*}\|u^{\prime}(x)-u^{\prime}(y)\| \leq \rho(\|x-y\|), \quad\text{if } x,y\in B_{1/2}.\end{align*} $$

The next result is a consequence of Corollary 1.6.

Corollary 1.7 [12, Theorem 4]

Let X be a two-dimensional normed space. The underlying norm on X is differentiable if and only if every AML function $u:X\to \mathbb {R}$ satisfying

$$ \begin{align*}|u(x)|\leq C(1+\|x\|), \quad\text{for all } x\in X,\end{align*} $$

for some $C>0$ , is linear.

Remark 1.8. The necessity of Corollary 1.7 follows from Savin’s proof in [12] and the fact that AML functions defined on the whole space are Lipschitz (Proposition 2.11). For the sufficiency, if the norm is not differentiable, let u be any AML function on X which is not differentiable everywhere; the existence of u is given by Corollary 2.9. This AML function has linear growth but is not linear.

This paper is organized as follows. In the next section we present some basic results on AML functions, several examples to motivate Question 1.2 and we introduce two moduli for the norm which turn out to be important tools to prove Theorem 1.5. Section 3 is devoted to Theorem 1.3. In Section 4 we prove Theorem 1.5.

We require the following notation. We denote by X and $X^{*}$ a finite-dimensional normed space and its dual space. By $\|\cdot \|$ we denote the norm of the underlying Banach space. Let $B_{r}(x)$ be the closed ball centered at $x\in X$ with radius equal to r. If x is the origin of X, we just write $B_{r}$ . For two functions $u,v:\Omega \subset X\to \mathbb {R}$ , we denote by $\{u<v\}$ the set $\{x\in \Omega :u(x)<v(x)\}$ . A function $u:\Omega \subset X\to \mathbb {R}$ is said K-Lipschitz if

$$ \begin{align*}|u(x)-u(y)|\leq K\|x-y\|,\quad\text{for all } x,y\in \Omega.\end{align*} $$

The Lipschitz constant of a function u, denoted by $\mathrm {Lip}(u)$ , is the lowest constant $K\geq 0$ such that u is K-Lipschitz. For two sets $V,\Omega \subset X$ , we write $V\subset \subset \Omega $ whenever V is compactly contained in $\Omega $ . For a set $U\subset X$ , we denote by $\overline {U}$ , $\text {int} (U)$ and $\partial U$ its closure, interior and boundary, respectively.

2 Preliminaries

This section is divided into three parts: we summarize some results of AML functions that can be found in the literature, we give some examples to motivate our results and we introduce two moduli of the norm which are used to prove Theorem 1.5. In the sequel, X denotes a finite-dimensional normed space and $\Omega $ a nonempty open subset of X.

2.1 Comparison with cones

The following geometric property is the main tool for working with AML functions.

Definition 2.1. Let $u:\Omega \subset X\to \mathbb {R}$ be a function. We say that u satisfies comparison with cones from above if for every bounded open set $V\subset \subset \Omega $ , every $x_{0}\in X$ and every $a,b\in \mathbb {R}$ for which

$$ \begin{align*}u(x)\leq C(x)= a+b\|x-x_{0}\| \end{align*} $$

holds in $\partial (V\setminus \{x_{0}\})$ , we have that $u\leq C$ in V as well. Analogously, we say that u satisfies comparison with cones from below if $-u$ satisfies comparison with cones from above. A function satisfies comparison with cones if it does so from above and below.

In fact, the property of comparison with cones characterizes AML functions.

Proposition 2.2 [3, Theorem 6.4]

Let $u:\Omega \subset X\to \mathbb {R}$ be a function. Then u enjoys comparison with cones if and only if it is AML.

The next result is a consequence of Proposition 2.2. Its proof follows without changes from its Euclidean counterpart found in [5].

Corollary 2.3 [5, Lemmas 2.4 and 2.7(i)]

Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function. Then, for $r<\mathrm {dist}(x,\partial \Omega )$ , the quantities

$$ \begin{align*}S^{+}(x,r):=\max_{y\in\partial B_{r}(x)}\dfrac{u(y)-u(x)}{r}\quad\text{and}\quad S^{-}(x,r):=-\min_{y\in\partial B_{r}(x)}\dfrac{u(y)-u(x)}{r} \end{align*} $$

are nonnegative. Moreover, for all $x\in \Omega $ , the functions $S^{+}(x,\cdot )$ and $S^{-}(x,\cdot )$ are nondecreasing in r and

$$ \begin{align*} \lim_{r\to 0}S^{+}(x,r)= \lim_{r\to 0}S^{-}(x,r).\end{align*} $$

If we denote by $S(x)=S_{u}(x)$ the common limit, we have

$$ \begin{align*}S(x)= \lim_{r\to 0} \sup_{y\in B_{r}(x) } \dfrac{u(y)-u(x)}{r}.\end{align*} $$

Notice that, since AML functions defined on open sets are locally Lipschitz, for any $r>0$ , the functions $S^{+}(\cdot ,r)$ and $S^{-}(\cdot ,r)$ are continuous in $\{x\in \Omega :\mathrm {dist}(x,\partial \Omega )>r\}$ .

Corollary 2.4. Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function and $R>0$ be such that ${B_{R}\subset \Omega }$ . Assume that $u=e_{0}^{*}$ on $B_{R}$ , where $e_{0}^{*}\in X^{*}$ and $e_{0}^{*}\ne 0$ . If $\|x_{0}\|=R$ , then $S(x_{0})>0$ .

Proof. Since $\text {int}(B_{\|x_{0}\|})\subset U$ , there exist $y\in \partial B_{1}$ and $t>0$ such that the segment $[x_{0},x_{0}+ty]$ is included in $B_{R}$ and $e_{0}^{*}(y)\ne 0$ . If $e_{0}^{*}(y)>0$ , then

$$ \begin{align*}S(x_{0})=\lim_{r\to 0} \max_{x\in \partial B_{r}(x_{0})}\dfrac{u(x)-u(x_{0})}{r}\ge\lim_{r\to 0}\dfrac{u(x_{0}+ry)-u(x_{0})}{r}= e_{0}^{*}(y)>0. \end{align*} $$

On the other hand, if $e_{0}^{*}(y)<0$ , then

$$ \begin{align*}S(x_{0})=-\lim_{r\to 0} \min_{x\in \partial B_{r}(x_{0})}\dfrac{u(x)-u(x_{0})}{r}\ge-\lim_{r\to 0}\dfrac{u(x_{0}+ry)-u(x_{0})}{r}=-e_{0}^{*}(y)>0.\\[-42pt]\end{align*} $$

Corollary 2.5. Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function. Assume that there exist $x\in \Omega $ , $W\subset \Omega $ a neighborhood of x and a function $f:W\to \mathbb {R}$ satisfying $u\leq f$ in W. Then $S(x)\leq \mathrm {Lip}(f)$ in the following cases:

1. (1) $f(\cdot )=u(x)+c\|\cdot -x\|$ for some $c>0$ , or

2. (2) f is an affine function on W and $f(x)=u(x)$ .

Proof. Both cases follow directly by computing $S(x)$ in terms of $S(x,\cdot )^{+}$ .

2.2 Examples of AML functions

Although simple, the following proposition allows us to give several examples of AML functions.

Proposition 2.6. Let $u:\Omega \subset X\to \mathbb {R}$ be a Lipschitz function. Assume that for every open set $V\subset \subset \Omega $ and for each $x\in V$ , there exist $x_{1},x_{2}\in \partial V$ , with $(x_{1},x_{2})$ included in V, such that $x\in (x_{1},x_{2})$ and $u|_{[x_{1},x_{2}]}$ is an affine function with slope equal to $\mathrm {Lip}(u)$ . Then u is AML.

Proof. If $\mathrm {Lip}(u)\equiv 0$ , the conclusion follows trivially. So, we assume that $\mathrm {Lip}(u)>0$ . Let $V\subset \subset \Omega $ be a bounded open set. Let $g:\overline {V}\to \mathbb {R}$ be a function such that g and u coincide in $\partial V$ . If $g\neq u$ , without loss of generality there exists $x\in V$ such that $g(x)>u(x)$ . Let $x_{1}, x_{2}\in \partial V$ be two vectors such that $x\in (x_{1},x_{2})\subset V$ , $u|_{[x_{1},x_{2}]}$ is an affine function of slope $\mathrm {Lip}(u)$ and $u(x_{2})>u(x)>u(x_{1})$ . Then we get

$$ \begin{align*}\mathrm{Lip}(g)\geq\dfrac{g(x)-g(x_{1})}{\|x-x_{1}\|}>\dfrac{u(x)-u(x_{1})}{\|x-x_{1}\|}=\mathrm{Lip}(u).\end{align*} $$

Therefore, u is an AML function.

Corollary 2.7. Let $P:\mathbb {R}^{n}\to \mathbb {R}$ and $Q:\mathbb {R}^{n}\to \mathbb {R}^{n-1}$ be the projections onto the first coordinate and onto the last $n-1$ coordinates, respectively. Let $u:(\mathbb {R}^{n},\|\cdot \|_{1})\to \mathbb {R}$ be a function defined by $u(x)= P(x)+ g\circ Q(x)$ , where $g:(\mathbb {R}^{n-1},\|\cdot \|_{1})\to \mathbb {R}$ is a $1$ -Lipschitz function. Then u is AML.

Proof. It is enough to apply Proposition 2.6 at segments included in lines of the form $x+\mathbb {R} e_{1}$ , with $x\in \mathbb {R}^{n}$ .

Corollary 2.8. Let $C\subset X$ be a closed convex set. Then the function $u:X\setminus C\to \mathbb {R}$ defined by $u(x)= \mathrm {dist}(x,C)$ is AML. In particular, the restriction of the norm $\|\cdot \|$ to $X\setminus \{0\}$ is $\|\cdot \|$ -AML.

Proof. Let $x\in X\setminus C$ and let $y_{x}\in C$ be one projection of x to C. That is, $\|x-y_{x}\| =\min \{\|x-z\|:z\in C\}$ . It is enough to apply Proposition 2.6 at segments included in half-lines of the form $y_{x}+\mathbb {R}_{+}(x-y_{x})$ , with $x\in X\setminus C$ .

Corollary 2.9. Let X be a finite-dimensional normed space with nondifferentiable norm. Then there exists a $\|\cdot \|$ -AML function $u:X\to \mathbb R$ such that $u(x)\le \| x\|$ for all $x\in X$ and u is not everywhere differentiable.

Proof. Since the norm is not differentiable, we can find a vector $z\in X$ of norm $1$ and two distinct functionals, $u_{1}^{*},u_{2}^{*}\in X^{*}$ , of norm $1$ such that $u_{1}^{*}(z)=u_{2}^{*}(z)=1$ . The function $u:=\max \{u_{1}^{*},u_{2}^{*}\}:X\to \mathbb {R}$ is not differentiable in the whole line $\mathbb {R} z$ and satisfies $u(x)\le \| x\|$ for all $x\in X$ . To see that u is AML, it is enough to apply Proposition 2.6 at segments included in lines of the form $x+\mathbb {R} z$ , with $x\in X$ .

Our final example shows that the set of smooth AML functions depends on the underlying norm.

Proposition 2.10. Let $p>2$ . The function $u:\mathbb {R}^{2}\setminus \{0\}\to \mathbb {R}$ defined by $u(x,y)=\|(x,y)\|_{p}$ is $\|\cdot \|_{p}$ -AML but not $\|\cdot \|_{2}$ -AML.

Proof. By Corollary 2.8, we already know that u is $\|\cdot \|_{p}$ -AML. Let us prove the second part of the proposition. Since $p>2$ , u is a $\mathcal {C}^{2}$ function. Then u is $\|\cdot \|_{2}$ -AML only if $\Delta _{\infty } u\equiv 0$ in the classical sense. However,

$$ \begin{align*} \Delta_{\infty} u((1/3)^{1/p},(2/3)^{1/p})= 3^{-4(({p-1})/{p})}2(p-1)(1+2^{2-{4}/{p}}-2^{2-{2}/{p}}), \end{align*} $$

which is $0$ only if $p=2$ .

The following proposition can be found in [10, Corollary 2.10] in the framework of $\text{AML}_{H}$ functions.

Proposition 2.11. Let X be a finite-dimensional normed space. Let $u:X\to \mathbb {R}$ be an AML function. Assume that there is $C>0$ such that $|u(x)|\leq C(1+\|x\|)$ for all $x\in X$ . Then u is Lipschitz.

Proof. Let us fix $x\in X$ . Then we have that

$$ \begin{align*}|u(y)-u(x)| \leq C(2+\|y\| +\|x\|)\leq C(3+2\|x\|)\leq 3C\|x-y\|,\!\!\quad\text{for all }y\in \partial B(x,\|x\|+1). \end{align*} $$

Therefore, by comparison with cones (Proposition 2.2), we have that

$$ \begin{align*}|u(y)-u(x)| \leq 3C\|x-y\|,\quad\text{for all }y\in B(x,\|x\|+1). \end{align*} $$

Since $x\in X$ is arbitrary, it follows that u is $3C$ -Lipschitz.

2.3 The moduli $\alpha $ and $\rho $

For $x^{*}\in X^{*}$ with $\|x^{*}\|=1$ , the face of the unit ball defined by $x^{*}$ is the set

$$ \begin{align*}F_{x^{*}}:=\{x\in X:x^{*}(x)=1\}\cap B_{1},\end{align*} $$

and for $\beta>0$ , the slice of the unit ball defined by $x^{*}$ and of depth $\beta $ is the set

$$ \begin{align*}S(x^{*},\beta):=\{x\in X:x^{*}(x)> 1-\beta\}\cap B_{1}\end{align*} $$

For $x^{*}\in X^{*}$ with $\|x^{*}\|=1$ and $\alpha>0$ , we consider the following union of faces:

$$ \begin{align*}H({x^{*},\alpha}):= \bigcup \{ F_{h^{*}}:\|h^{*}-x^{*}\|\leq \alpha,~\|h^{*}\|=1\}\subset \partial B_{1}.\end{align*} $$

For $x^{*}\in X^{*}\setminus \{0\}$ , we define $H({x^{*},\alpha }):= H({x^{*}/\|x^{*}\|,\alpha })$ . The set $H({x^{*},\alpha })$ is a compact subset of $X^{*}$ . We now define, for $x^{*}$ a unit vector of $X^{*}$ and $\beta>0$ ,

$$ \begin{align*}\alpha(x^{*},\beta) :=\sup\{\alpha\in\mathbb{R}:H(x^{*},\alpha)\subset S(x^{*},\beta)\}\end{align*} $$

and $\alpha (\beta ):= \inf \{\alpha (x^{*},\beta ):\|x^{*}\|=1\}$ . Also, for $x^{*}\in X^{*}$ , with $\|x^{*}\|=1$ , and $\sigma>0$ , we define

$$ \begin{align*}\rho(x^{*},\sigma):= \sup\{\rho:S(x^{*},\rho)\cap \partial B_{1}\subset H(x^{*},\sigma)\}\end{align*} $$

and $\rho (\sigma ):=\inf \{\,\rho (x^{*},\sigma ):\|x^{*}\|=1\}$ .

Let us present two examples. If X is a Euclidean space, then $\alpha (x^{*},\beta )=(2\beta )^{1/2}$ for every unit vector $x^{*}$ and $\beta \in (0,2)$ . If $X=(\mathbb {R}^{2},\|\cdot \|_{\infty })$ and $x^{*}$ is the unit linear form defined by $x^{*}((x_{1},x_{2}))=x_{1}$ , then $\alpha (x^{*},\beta )=2$ for every $\beta>0$ . The next proposition generalizes the first example.

Proposition 2.12. Let X be a finite-dimensional normed space with differentiable norm. Then, for any unit vector $x^{*}\in X^{*}$ , $\lim _{\beta \to 0} \alpha (x^{*},\beta )=0$ . In particular, $\lim _{\beta \to 0} \alpha (\beta )=0$ .

Proof. Let $x^{*}\in X^{*}$ of norm $1$ and let $\varepsilon>0$ . Let $y^{*}\in X^{*}$ be such that $\|x^{*}-y^{*}\|=\varepsilon $ and $\|y^{*}\|=1$ . Since X is a finite-dimensional normed space, $F_{y^{*}}$ is compact. Moreover, since the norm is differentiable, $F_{x^{*}}\cap F_{y^{*}}=\emptyset $ . By continuity of $x^{*}$ and compactness of $F_{y^{*}}$ , there exists $c>0$ such that

$$ \begin{align*}\max\{x^{*}(y):y\in F_{y^{*}}\}= 1-c.\end{align*} $$

Thus, if $\beta <c$ , $ F_{y^{*}}\not \subset S(x^{*},\beta )$ , and since $F_{y^{*}}\subset H(x^{*},\varepsilon )$ , we get

$$ \begin{align*} H(x^{*},\varepsilon)\not\subset S(x^{*},\beta).\end{align*} $$

Thus, $\alpha (x^{*},\beta )\leq \varepsilon $ whenever $\beta <c$ .

The following propositions are used in the proof of Theorem 1.5.

Proposition 2.13. Let X be a finite-dimensional normed space. Then $\alpha (\beta )\geq \beta>0$ for every $\beta\in (0,2)$ .

Proof. Let $x^{*},y^{*}\in X^{*}$ be unit linear forms such that $\|x^{*}-y^{*}\|< \beta $ . Then

$$ \begin{align*}x^{*}(y)=y^{*}(y)+(x^{*}-y^{*})(y)> 1-\beta, \quad\text{for all }y\in F_{y^{*}}.\end{align*} $$

Thus, $F_{y^{*}}\subset S(x^{*},\beta )$ and therefore, $\alpha (x^{*},\beta )\geq \beta $ .

Proposition 2.14. Let X be a finite-dimensional normed space with differentiable norm. For any $\sigma>0$ , $\rho (\sigma )>0$ . Therefore, for any unit vector $x^{*}\in X^{*}$ , and for any unit vector $x\in X\setminus H(x^{*},\sigma )$ , $x^{*}(x)\le 1-\rho (\sigma )$ holds.

Proof. Let $\sigma>0$ . Notice that, if $\sigma \geq 2$ , there is nothing to prove since $H(x^{*},\sigma )=\partial B_{1}$ for any $\|x^{*}\|=1$ . So, we assume that $\sigma <2$ . Let $x^{*}\in X^{*}$ with $\|x^{*}\|=1$ .

Step 1: $\rho (x^{*},\sigma )>0$ . Let us define

$$ \begin{align*}G:= \bigcup \{F_{y^{*}}:\|y^{*}\|=1\quad \text{and}\quad \|x^{*}-y^{*}\| \geq \sigma\}.\end{align*} $$

Clearly, G is a compact set which depends on $x^{*}$ and $\sigma $ . Since X has differentiable norm, we have that $F_{x^{*}}\cap G=\emptyset $ . Therefore, there exists $\rho>0$ such that

$$ \begin{align*} \max\{x^{*}(h):h\in G\}:= 1-\rho.\end{align*} $$

Thus, $\rho (x^{*},\sigma )\geq \rho>0$ .

Step 2. For any $x^{*}\in X^{*}$ unit linear form, there exist $\delta>0$ and $c>0$ such that

$$ \begin{align*}\rho(y^{*},\sigma)>c\quad\text{for all } y^{*}\quad \text{such that}\ \|y^{*}-x^{*}\|<\delta\quad \text{and}\quad \|y^{*}\|=1.\end{align*} $$

Indeed, let $x^{*}\in X^{*}$ with $\|x^{*}\|=1$ . Let $\varepsilon \in (0,\sigma )$ . By Step $1$ , we know that $\rho :=\rho (x^{*},\sigma -\varepsilon )>0$ and that $S(x^{*},\beta )\cap \partial B_{1}\subset H(x^{*},\sigma -\varepsilon )$ whenever $\beta <\rho $ . Define $\delta :=\min \{\rho /2,\varepsilon \}$ . If $\|x^{*}-y^{*}\|<\delta $ , with $\|y^{*}\|=1$ , and if $\beta =\rho /2+\|x^{*}-y^{*}\|$ , we get that

$$ \begin{align*}S(y^{*},\rho/2)\cap \partial B_{1}\subset S(x^{*},\beta)\cap \partial B_{1}\subset H(x^{*},\sigma-\varepsilon)\subset H(y^{*},\sigma).\end{align*} $$

Therefore,

$$ \begin{align*}\rho(y^{*},\sigma)\geq \dfrac{\rho}{2}>0,\quad\text{whenever }\|x^{*}-y^{*}\|< \delta. \end{align*} $$

Step 3: $\rho (\sigma )>0$ . Since X is finite-dimensional, the conclusion follows directly from the compactness of the unit sphere of $X^{*}$ and Step $2$ .

3 Proof of Theorem 1.3

This section is devoted to proving Theorem 1.3. In our proof we mainly follow the ideas of [4] where we can find the proof of the theorem whenever X is a Euclidean space. Let us start with some geometric facts which allow us to avoid the Euclidean arguments used in the aforementioned work. We point out that Propositions 3.1 and 3.3 below hold true in general Banach spaces. Recall that, for $x\in X$ and $r>0$ , $B_{r}(x)$ and $B_{r}$ stand for the closed ball of radius r centered at x and at the origin, respectively.

Proposition 3.1. Let X be a normed space. Let $x\in \partial B_{1}$ and let $V= \partial B_{1}\cap \partial B_{2}(x)$ . Then, for all $y\in V$ , the segment $[-x,y]$ is contained in V.

Proof. Let $y\in V$ . Since $B_{1}\subset B_{2}(x)$ , there exists a closed hyperplane $\{f^{*}=1\}$ which is tangent at y to both $B_{1}$ and $B_{2}(x)$ simultaneously. Observe that this implies that $\|f^{*}\|=1$ , $f^{*}(y)=1$ , $\|y\|=1$ and $f^{*}(y-x)=2$ . Hence, we conclude that $f^{*}(-x)=1$ . Now let $z\in [-x,y]$ . Therefore, there is $\lambda \in [0,1]$ such that $z=\lambda (-x)+(1-\lambda )y$ . By the triangle inequality, we obtain that $\|z\|\leq 1$ and $\|z-x\|\leq 2$ . By linearity of $f^{*}$ , we get that $f^{*}(z)=1$ and $f^{*}(z-x)=2$ . Therefore, $z\in V$ .

Remark 3.2. In Proposition 3.1, if X has a differentiable norm, then $f^{*}$ is unique. Indeed, it must be the support functional of $-x$ . Therefore, V is contained in $\{f^{*}=1\}$ .

Before stating the next proposition, we recall that in finite-dimensional normed spaces the notions of Gâteaux differentiability and Fréchet differentiability coincide for convex functions. Therefore, the following proposition can be used, for instance, in finite-dimensional normed spaces with differentiable norm.

Proposition 3.3. Let X be a Banach space. Let $u^{+},u^{-}\in S_{X}$ be such that the norm is Gâteaux differentiable at $u^{+}$ and $u^{-}$ with differentials $u^{*}$ and $-u^{*}$ , respectively. Let $f:X\to \mathbb {R}$ be a $1$ -Lipschitz function such that $f(tu^{+})=t$ and $f(tu^{-})=-t$ for all $t\geq 0$ . Then $f\equiv u^{*}$ .

Proof. First case. Let us start with $v\in \ker (u^{*})$ . By the differentiability of the norm, there exists a sequence $(\varepsilon _{n})_{n}\subset \mathbb {R}^{+}$ which tends to $0$ as n tends to infinity and such that the expression

$$ \begin{align*}\max\{|\|nu^{+}- v\|-\|nu^{+}\||,|\|nu^{-}- v\|-\|nu^{-}\||\}\leq \varepsilon_{n} \end{align*} $$

holds true for all $n\in \mathbb {N}$ . Now, if n is large enough, $n>f(v)$ and then

$$ \begin{align*}1\geq\dfrac{f(nu^+)-f(v)}{\|nu^+-v\|}\geq\dfrac{n-f(v)}{n+\varepsilon_n},\end{align*} $$

which implies $f(v)\geq -\varepsilon _{n}$ for all large n. Thus, $f(v)\geq 0$ . For the reverse inequality, observe that

$$ \begin{align*}1\geq \dfrac{|f(nu^-)-f(v)|}{\|nu^--v\|}\geq\dfrac{n+f(v)}{n+\varepsilon_n}\end{align*} $$

holds true for all $n>0$ . Finally, we arrive at $f(v)\leq \varepsilon _{n}$ , for all $n>0$ . Therefore, $f(v)\leq 0$ , implying that $f(v)=0$ .

Second case, Let $v\in X\setminus \ker (u^{*})$ . Without loss of generality, assume that $u^{*}(v)=\alpha >0$ . Let us consider the function $g:X\to \mathbb {R}$ defined by $g(x)=f(x+\alpha u^{+})-\alpha $ . Clearly, g is a $1$ -Lipschitz function such that $g(tu^{+})=t$ for all $t\geq 0$ . We claim that $g(tu^{-})= -t$ for all $t>0$ . Indeed, let us fix $t>0$ . For $s>0$ , we have that $u^{*}(-\alpha u^{+}+ su^{-})=-\alpha -s$ . Thus, $\|-\alpha u^{+}+ su^{-}\|=\alpha +s$ . Also, since $g(0)=0$ , $g(-\alpha u^{+}+ su^{-})=-\alpha -s$ and g is $1$ -Lipschitz, g must be linear along the segment $[0,-\alpha u^{+} +su^{-}]$ , that is,

$$ \begin{align*}g(\lambda (-\alpha u^{+}+ su^{-}))= -\lambda(\alpha+s),\quad\text{for all } \lambda\in [0,1], \quad\text{for all }s>0.\end{align*} $$

If $s>t$ , we can set $\lambda =t/s$ . Using the continuity of g, sending s to infinity, we get that $g(tu^{-})=-t$ . Finally, the function g satisfies the hypothesis to apply the first case at the vector $v-\alpha u^{+}\in \ker (u^{*})$ . Hence, we get that $g(v-\alpha u^{+})=0$ . Thus, by definition of g, $f(v)=\alpha $ , finishing the proof.

The next corollary corresponds to the property used in [4], where X is a finite-dimensional Euclidean space.

Corollary 3.4. Let X be a Banach space. Let $u\in \partial B_{1}$ be such that the norm is Gâteaux differentiable at u with differential $u^{*}$ . Let $f:X\to \mathbb {R}$ be a $1$ -Lipschitz function such that $f(tu)=t$ for all $t\in \mathbb {R}$ . Then $f\equiv u^{*}$ .

Let us continue with the following lemma.

Lemma 3.5. Let X be a finite-dimensional Banach space and let $\Omega $ be a nonempty open subset of X. Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function and let $x\in \Omega $ . Then the following assertions are equivalent.

1. (i) For each $r\in (0,\mathrm {dist}(x,\partial \Omega ))$ , there exists a vector $e_{x,r}^{*} \subset X^{*}$ , with $\|e_{x,r}^{*}\|=S(x)$ , such that

   $$ \begin{align*}\max_{y\in \overline{B}_{r}(x)}\dfrac{|u(y)-u(x)-e^{*}_{x,r}(y-x)|}{r}\rightarrow 0\quad\text{as }r\rightarrow 0.\end{align*} $$

2. (ii) For any decreasing sequence $(r_{j})_{j}$ , convergent to $0$ , there are a subsequence $(r_{j(k)})_{k}$ and $e^{*}\in X^{*}$ , with $\|e^{*}\|=S(x)$ , such that

   $$ \begin{align*}\max_{y\in \overline{B}_{r_{j(k)}}(x)}\dfrac{|u(y)-u(x)-e^{*}(y-x)|}{r_{j(k)}}\rightarrow 0 \quad\text{as }k\rightarrow \infty.\end{align*} $$

Proof. (i) $\Rightarrow $ (ii). This is due to the compactness of closed bounded subsets of $X^{*}$ .

(ii) $\Rightarrow $ (i). Reasoning by contradiction, if (i) does not hold true, then there are $\varepsilon>0$ and a sequence $(r_{j})_{j}$ , convergent to $0$ , such that

$$ \begin{align*}\max_{y\in \overline{B}_{r_{j}}(x)}\dfrac{|u(y)-u(x)-e^{*}(y-x)|}{r_{j}}\geq \varepsilon \quad\text{for all }j\in\mathbb{N}, \quad\text{for all } e^{*}\in X^{*},~\|e^{*}\|=S(x).\end{align*} $$

This clearly contradicts statement (ii).

We can now provide the proof of Theorem 1.3.

Proof of Theorem 1.3

Let $x\in \Omega $ . We prove Lemma 3.5(ii). Let $(r_{j})_{j}\subset \mathbb {R}^{+}$ be a sequence that converges to $0$ . For each $j\in \mathbb {N}$ , let us define $v_{j}:r_{j}^{-1}(\Omega -x)\to \mathbb {R}^{*}$ by

$$ \begin{align*}v_{j}(y)=\dfrac{u(x+r_{j}y)-u(x)}{r_{j}}.\end{align*} $$

For each compact subset K of X, the functions $v_{j}$ are well defined on K for j large enough. Since u is a locally Lipschitz function, the $(v_{j})_{j}|_{K}$ form an equi-Lipschitz family vanishing at $0$ . So by the Arzelà–Ascoli theorem, up to a subsequence, we can assume that the sequence $(v_{j})$ converges uniformly on compact subsets of X towards a Lipschitz function v vanishing at $0$ , that is, $v(y)=\lim _{j} v_{j}(y)$ for any $y\in X$ . If v is linear, then we can take $e^{*}=v$ .

So, to prove Theorem 1.3, it remains only to show that v is necessarily linear. Let $S(x)$ be computed with the function u (see Corollary 2.3). Since a locally uniform limit of functions satisfying comparison with cones satisfies comparison with cones, we can apply Corollary 2.3 on v as well. From now on, we define the quantities

$$ \begin{align*}L^{+}(y,r):=\max_{z\in\partial B_{r}(y)}\dfrac{v(z)-v(y)}{r}, \quad L^{-}(y,r):=-\min_{z\in\partial B_{r}(y)}\dfrac{v(z)-v(y)}{r}, \end{align*} $$

for $y\in X$ and $r>0$ . Also, we define the corresponding values

$$ \begin{align*}L^{+}(y)=\lim_{r\to 0}L^{+}(y,r),\quad L^{-}(y)=\lim_{r\to 0}L^{-}(y,r),\end{align*} $$

where $L(y)=L^{+}(y)=L^{-}(y)$ , by Corollary 2.3.

Proposition 3.6. Assume that $\max \{L^{-}(y,r), L^{+}(y,r)\}\leq S(x)$ for all $r>0$ and for all $y\in X$ . Further, assume that $L^{+}(0)=S(x)=L^{-}(0)$ . Then v is linear.□

Proof. The first assumption implies that $\mathrm {Lip}(v)\leq S(x)$ . Thanks to the monotonicity of $L^{\pm }(0,\cdot )$ (see Corollary 2.3) and the second assumption, we get that $S(x)\leq \min \{L^{-}(0,r), L^{+}(0,r)\}$ , and therefore, $S(x) =L^{+}(0,r)=L^{-}(0,r)$ . Further, this implies that $\mathrm {Lip}(v)\geq S(x)$ , and then $\mathrm {Lip}(v)= S(x)$ . By continuity of v and compactness of closed bounded sets, we can find $z_{r}^{+},z_{r}^{-}\in \partial B_{r}$ such that

$$ \begin{align*}L^{\pm}(0,r)=\pm\dfrac{v(z_{r}^{\pm})-v(0)}{r}=\pm\dfrac{v(z_{r}^{\pm})}{r}.\end{align*} $$

Therefore,

$$ \begin{align*}L^{+}(0,r)=L^{-}(0,r)=S(x)= \dfrac{v(z_{r}^{+})-v(z_{r}^{-})}{2r}.\end{align*} $$

Observe that the function v is an $S(x)$ -Lipschitz function such that

(3-1) $$ \begin{align} v(z_{r}^{+})-v(z_{r}^{-})=2S(x)r\leq S(x)\|z_{r}^{+}-z_{r}^{-}\|. \end{align} $$

Since $z_{r}^{+},z_{r}^{-}\in \partial B_{r}$ , $\|z_{r}^{+}-z_{r}^{-}\|\leq 2r$ , and applying (3-1), we get that $\|z_{r}^{+}-z_{r}^{-}\|=2r$ and that v is an affine function on $[z_{r}^{-},z_{r}^{+}]$ . Moreover, since $v(0)=0$ , we have that $v(z_{r}^{+})=S(x)r$ and $v(z_{r}^{-})=-S(x)r $ .

Let $u^{*}\in X^{*}$ be the linear form of norm $1$ such that $u^{*}(z^{+}_{1})=1$ . By Proposition 3.1 and Remark 3.2, we deduce that $u^{*}(z^{-}_{1})=-1$ . Indeed, if $u^{*}(z^{-}_{1})<-1$ , then $z^{-}_{1}\notin \partial B_{1}\cap \partial B_{2}(z^{+}_{1})$ . Thus, $\|z_{1}^{+}-z_{1}^{-}\|< 2$ , a contradiction since $\mathrm {Lip}(v)= S(x)$ . Let $r>1$ . Let us show that $u^{*}(z^{+}_{r})=r$ . Indeed, since $v(0)=0$ , $v(z^{+}_{r})=S(x)r$ and v is $S(x)$ -Lipschitz, v must be linear along the segment $[0,z^{+}_{r}]$ . Therefore, the vector $z^{+}_{r}/\|z^{+}_{r}\|$ may take the place of $z^{+}_{1}$ because $v(z^{+}_{r}/\|z^{+}_{r}\|)=S(x)$ . If $u^{*}(z^{+}_{r})<r$ , then $u^{*}(z^{+}_{r}/\|z^{+}_{r}\|)<1$ . By Proposition 3.1 and Remark 3.2, we get that

$$ \begin{align*}\bigg\|z_{1}^{-} - \dfrac{z^{+}_{r}}{\|z^{+}_{r}\|}\bigg\|<2,\end{align*} $$

a contradiction since $\mathrm {Lip}(v)= S(x)$ . As a direct consequence of $u^{*}(z^{+}_{r})=r$ we get that $u^{*}(z^{-}_{r})=-r$ .

Since X is a finite-dimensional space, there exist a sequence $(r(n))_{n}\subset \mathbb {R}^{+}$ which goes to infinity and two vectors $q^{+},q^{-}\in \partial B_{1}$ such that

$$ \begin{align*}\lim_{n\to\infty}\dfrac{z^{\pm}_{r(n)}}{\|z^{\pm}_{r(n)}\|}= q^{\pm}.\end{align*} $$

Clearly $u^{*}(q^{+})=1$ and $u^{*}(q^{-})=-1$ . As a consequence of the continuity of v and its linear behavior along the lines $[0,z^{+}_{r(n)}]$ , with slope $S(x)$ , we get that $v(tq^{+})=tS(x)$ for all $t\geq 0$ . Analogously, we get that $v(tq^{-})=-tS(x)$ . Finally, applying Proposition 3.3, we conclude that $v=S(x)u^{*}$ .

To finish the proof of Theorem 1.3, it remains only to prove the hypotheses of Proposition 3.6. We point out that this part of the proof follows as in the proof given in [4], where X is a Euclidean space.

To this end, let us start with the case of the superscript $+$ . Let $y\in X$ and $z\in \partial B_{r}(y)$ be such that

(3-2) $$ \begin{align} L^{+}(y,r)=\dfrac{v(z)-v(y)}{r}=\lim_{j\to\infty}\dfrac{u(r_{j}z+x)-u(r_{j}y+x)}{r_{j}r}. \end{align} $$

Since $r_{j}z\in \partial B_{r_{j}r}(r_{j}y)$ , we get that

(3-3) $$ \begin{align} \dfrac{u(r_{j}z+x)-u(r_{j}y+x)}{r_{j}r}\leq S^{+}(r_{j}y+x,r_{j}r)\leq S^{+}(r_{j}y+x,R), \end{align} $$

for $r_{j}r<R<\mathrm {dist}(r_{j}y+x,\partial U)$ . Notice that in (3-3), the first and second inequalities are due to the definition of $S^{+}$ and to Corollary 2.3, respectively. Combining (3-2), (3-3) and using the continuity of the function $S^{+}(\cdot ,R)$ , we get that

$$ \begin{align*}L^{+}(y,r)\leq \lim_{j\to\infty} S^{+}(r_{j}y+x,R)\leq S^{+}(x,R).\end{align*} $$

Finally, sending R to $0$ , we obtain that $L^{+}(y,r)\leq S(x)$ . To prove the second hypothesis, let us consider $y=0$ . Then we compute

$$ \begin{align*}L^{+}(0,r)= \max_{z\in \partial B_{r}}\dfrac{v(z)}{r}=\max_{z\in \partial B_{r}}\lim_{j\to \infty}\dfrac{u(r_{j}z+x)-u(x)}{r_{j}r}.\end{align*} $$

By compactness of $\partial B_{r}$ and continuity of u, for each j there exists $z_{j}\in \partial B_{r}$ satisfying

$$ \begin{align*}u(r_{j}z_{j}+x)=\max_{z\in \partial B_{r}}u(r_{j}z+x).\end{align*} $$

Let us consider any cluster point $\overline {z}$ of $(z_{j})_{j}\subset \partial B_{r}$ . Let $(j(n))$ be a subsequence such that $z_{j(n)}\to \overline {z}$ . Using the fact that u is Lipschitz in a neighborhood of x, we prove that

$$ \begin{align*}L^{+}(0,r)&\geq \lim_{n\to \infty}\dfrac{u(r_{j(n)}\overline{z}+x)-u(x)}{r_{j(n)}r}\\ &=\lim_{n\to \infty}\max_{z\in \partial B_{r}}\dfrac{u(r_{j(n)}z+x)-u(x)}{r_{j(n)}r}=\lim_{n\to \infty}S^{+}(x,r_{j(n)}r)=S(x).\end{align*} $$

Therefore, sending r to $0$ , we get that $L^{+}(0)\geq S(x)$ . Thus, $L^{+}(0)=S(x)$ . The case with superscript $-$ is analogous. This concludes the proof of Theorem 1.3.□

4 Proof of Theorem 1.5

Savin, in [12], has shown that every planar AML function is continuously differentiable whenever the underlying space is endowed with a Euclidean norm. In what follows, we generalize the technique developed in the aforementioned paper to prove Theorem 1.5. For the sake of completeness, we provide the proofs of Proposition 4.1 and Lemma 4.4 which follow without significant changes from the work [12].

From now on, X denotes a two-dimensional Banach space endowed with a differentiable norm. The proof of Theorem 1.5 uses Theorem 1.3 and the following two propositions.

Proposition 4.1 [12, Lemma 1]

Let $u:\Omega \subset X\to \mathbb {R}$ be an AML function where $\Omega $ is an open and convex set containing $0$ , and u does not coincide with an affine function on any neighborhood of $0$ . Then, for every open subset W of $\Omega $ containing $0$ . there exist $y\in W$ and an affine function $g:=e^{*}+u(y)-e^{*}(y)$ , where $e^{*}\in X^{*}$ satisfies $\|e^{*}\|=S(y)$ , such that one of the sets $\{u>g\}$ and $\{u<g\}$ has at least two distinct connected components intersecting W.

Proof. Let W be an open subset of $\Omega $ containing $0$ . Then there exists a segment $[z_{1},z_{2}]\subset W$ such that u is not an affine function on $[z_1,z_2]$ . Thus, there is an affine function $\ell $ on $[z_{1},z_{2}]$ and a point $y\in (z_{1},z_{2})$ such that $u(y)=\ell (y)$ and

$$ \begin{align*} u\geq \ell \text{ in }[z_{1},z_{2}] \text{ and } u(z_{i})> \ell(z_{i}), \text{ for }i=1,2,&\quad\text{or}\\ u\leq \ell \text{ in }[z_{1},z_{2}] \text{ and } u(z_{i})< \ell(z_{i}), \text{ for }i=1,2.& \end{align*} $$

We treat the first case; the second is similar. From Theorem 1.3, there exist vectors $e_{y,r}^{*}$ such that $\|e_{y,r}^{*}\|=S(y)$ and

$$ \begin{align*}\lim_{r\to 0}\max_{x\in B_{r}(y)} \dfrac{|u(x)-u(y)-e_{y,r}^{*}(x-y)|}{r}= 0.\end{align*} $$

By compactness, there is a sequence $(r_{i})_{i}$ , which converges to $0$ , such that $e_{y,r_{i}}^{*}\to e^{*}$ . Therefore, $\|e^{*}\|= S(y)$ and

(4-1) $$ \begin{align} \lim_{i\to\infty}\max_{x\in B_{r_{i}}(y)} \dfrac{|u(x)-g(x))|}{r_{i}}= 0, \end{align} $$

where g is the affine function defined by $g(x)=e^{*}(x)-e^{*}(y)+u(y)$ . Since $u\geq \ell $ in $[z_{1},z_{2}]$ and $u(y)=\ell (y)$ , the limit (4-1) implies that g coincides with $\ell $ in $[z_{1},z_{2}]$ , and then $z_{1},z_{2}\in \{u>g\}$ .

Reasoning by contradiction, suppose that there exists a polygonal line $\gamma \subset \{u>g\}$ connecting the points $z_{1}$ and $z_{2}$ . Let $\Gamma $ be the union of $\gamma $ with the segment $[z_{1},z_{2}]$ , and U be the union of all bounded connected components of $X\setminus \Gamma $ . Let $h^{*}\in X^{*}$ be a nonzero linear form such that $h^{*}(z_{2}-z_{1})=0$ . Using the fact that $y\notin \gamma $ and replacing $h^{*}$ by $-h^{*}$ if necessary, there exists $\delta>0$ such that $B_{\delta }(y)\cap \{h^{*}>0\}\subset U$ . Since $\gamma $ is compactly contained in $\{u> g\}$ , there exists $\varepsilon>0$ such that $u\geq g+\varepsilon h^{*}$ on $\gamma $ , hence also on $\Gamma $ . We have $u\geq g+\varepsilon h^{*}$ on $\partial U\subset \Gamma $ . Since u is an AML function, $u\geq g+\varepsilon h^{*}$ on U, so $u-g\geq \varepsilon h^{*}$ on $B_{\delta }(y)\cap \{h^{*}>0\}$ . This contradicts the limit (4-1), finishing the proof.

The assumptions of the following proposition are explained by the conclusions of Theorem 1.3 and Proposition 4.1.

Proposition 4.2. Let $\rho>0$ . Let $u:\text {int}(B_{\rho })\subset X\to \mathbb {R}$ be an AML function and let $e_{1}^{*}\in X^{*}$ such that

$$ \begin{align*}\sup \{|u(x)-e_{1}^{*}(x)|,~x\in \text{int}(B_{\rho})\}\leq \lambda\rho\|e^{*}_{1}\|.\end{align*} $$

Further, assume that there exists $e^{*}\in X^{*}$ such that $\{u>e^{*}\}$ has at least two distinct connected components that intersect $B_{\rho /6}$ . Then, for $\varepsilon>0$ , there exists $\lambda (\varepsilon )>0$ such that if $\lambda \leq \lambda (\varepsilon )$ , then

$$ \begin{align*}\|e^{*}-e_{1}^{*}\|\leq \varepsilon \|e^{*}_{1}\|.\end{align*} $$

Proof. If $e_{1}^{*}=0$ , then u is identically $0$ in $\text {int}(B_{\rho })$ . Therefore, the second hypothesis cannot occur. So, without loss of generality, we assume that $e_{1}^{*}\neq 0$ . Let $R=C(\varepsilon ,X)>0$ be given by Lemma 4.3. Let us define $\displaystyle \lambda (\varepsilon ):={1}/{6C(\varepsilon ,X)}$ . If $w:\text {int}(B_{6R})\to \mathbb {R}$ is the function defined by

$$ \begin{align*}w(x):= \dfrac{6R}{\rho\|e^{*}_{1}\|}u\bigg( \dfrac{\rho x}{6R} \bigg),\end{align*} $$

and if $\lambda <\lambda (\varepsilon )$ , the function w satisfies the following assertions.

1. (a) $\sup \{|w(x)-{e_{1}^{*}(x)}/{\|e^{*}_{1}\|}|:x\in \text {int}(B_{6R})\}\leq 1$ .

2. (b) The set $\{w>{e^{*}}/{\|e^{*}_{1}\|}\}$ has at least two distinct connected components that intersect $B_{R}$ .

Therefore, Proposition 4.2 follows from Lemma 4.3.

Lemma 4.3. For every $\varepsilon>0$ , there exists a constant $C(\varepsilon ,X)>0$ with the following property. Let $\varepsilon>0$ , $R\geq C(\varepsilon ,X)$ and $u:\text {int}(B_{6R})\to \mathbb {R}$ be an AML function satisfying the following assertions.

• (H1) $\sup \{|u(x)-e_{1}^{*}(x)|: x\in \text {int}(B_{6R})\}\leq 1$ for some $\|e_{1}^{*}\|=1$ ,

• (H2) There exists a linear form $e^{*}\in X^{*}$ such that the set $\{u>e^{*}\}$ has at least two distinct connected components that intersect $B_{R}$ .

Then

$$ \begin{align*}\|e^{*}-e^{*}_{1}\|\leq \varepsilon.\end{align*} $$

Proof of Lemma 4.3

Let $f^{*}=e_{1}^{*}-e^{*}$ and let $\varepsilon>0$ . Without loss of generality, assume that $f^{*}\ne 0$ . By (H1), we have that

$$ \begin{align*} &\{f^{*}<-1\}\cap \text{int}(B_{6R})\subset \{u<e^{*}\},\\ &\{f^{*}>1\}\cap \text{int}(B_{6R})\subset \{u>e^{*}\}. \end{align*} $$

Thus, by hypothesis (H2), we can find a connected component $\mathcal {U}$ of $\{u>e^{*}\}$ that intersects $B_{R}$ and that is included in the strip $\mathcal {S}:=\{|f^{*}|\leq 1\}$ of width $2\|f^{*}\|^{-1}$ . If $R> \|f^{*}\|^{-1}$ , the set $\mathcal {S}\cap \partial B_{R}$ is the union of two disjoint arcs of $\partial B_{R}$ . Observe that $\mathcal {U}$ cannot be compactly contained in $\text {int}(B_{6R})$ . Otherwise, it would contradict the AML property of u (comparing against $e^{*}$ on $\overline {\mathcal {U}}$ ). Consider a polygonal line $\Gamma \subset \mathcal {U}\subset \mathcal {S}$ that starts in $B_{R}$ and exits $B_{6R}$ . Let $x_{0}\in X$ be a vector such that $\|x_{0}\|=3R$ and $f^{*}(x_{0})=0$ . Replacing $x_{0}$ by $-x_{0}$ if necessary, we can assume that $\Gamma $ intersects the two distinct arcs of $\mathcal {S}\cap \partial B_{R}(x_{0})$ . Let $v:B_{2R}\to \mathbb {R}$ be the function defined by $v(\cdot ):=u(\cdot +x_{0})-e_{1}^{*}(x_{0})$ . Observe that by (H1),

$$ \begin{align*}|v(x)-e_{1}^{*}(x)|\leq |u(x+x_{0})-e_{1}^{*}(x_{0}+x)|\leq 1,\quad\text{for all } x\in B_{2R},\end{align*} $$

and that, due to the fact that $f^{*}(x_{0})=0$ , $y\in \{v>e^{*}\}$ if and only if $y+x_{0}\in \{u>e^{*}\}$ . Therefore, replacing u by v (and $x_{0}$ by $-x_{0}$ if necessary), hypotheses (H1) and (H2) imply the following assertions.

1. (H1′) $\max \{|u(x)-e_{1}^{*}(x)|:x\in B_{2R}\}\leq 1$ for some $\|e_{1}^{*}\|=1$ .

2. (H2′) If $R>\|f^{*}\|^{-1}=\|e_{1}^{*}-e^{*}\|^{-1}$ , the set $\{u>e^{*}\}\cap B_{2R}$ has a connected component $\mathcal {U}$ , included in $\mathcal {S}=\{|f^{*}|\leq 1\}$ , that contains a polygonal line $\Gamma $ connecting the two distinct arcs of $\mathcal {S}\cap \partial B_{R}$ .

Lemma 4.3 follows from the next two lemmas.

Lemma 4.4 [12, Lemma 3]

Let $0<\gamma <1$ . If $R\geq C_{1}(\gamma ):=20\gamma ^{-2}$ , then

$$ \begin{align*}\|e^{*}\|\geq 1-\gamma.\end{align*} $$

Lemma 4.5. Let u be AML satisfying (H1 $^{\prime }$ ) and (H2 $^{\prime }$ ), let $\|e^{*}\|\geq \gamma>0$ and $\beta>0$ . There exists $C_{2}=C_{2}(\gamma ,\beta )$ such that if $R\geq C_{2}$ , then

$$ \begin{align*}\inf \bigg\{|f^{*}(h)|:h\in H\bigg(e^{*},\dfrac{\beta}{2}\bigg) \bigg\}< \gamma.\end{align*} $$

Let us finish the proof of Lemma 4.3. Since X is a finite-dimensional space with differential norm, $X^{*}$ is uniformly convex. Hence, there exists $\sigma (\varepsilon )>0$ such that for any two unit vectors $x^{*},y^{*}$ in $X^{*}$ satisfying $\| ({x^{*}+y^{*}})/{2}\|>\sigma (\varepsilon )$ , we have $\|x^{*}-y^{*}\| <\varepsilon $ . If $\gamma ,\beta>0$ are small, we have

(4-2) $$ \begin{align} \beta+\gamma<1-\sigma(\varepsilon/2) \end{align} $$

and

(4-3) $$ \begin{align} \dfrac{\beta}{2}+\dfrac{\gamma+\beta}{1-\beta}<\dfrac{\varepsilon}{2}. \end{align} $$

Let us fix $\beta =\beta (\varepsilon )$ and $\gamma =\gamma (\varepsilon )$ satisfying (4-2) and (4-3), and define $C(\varepsilon ,X):=\max \{C_{1}({\gamma }),C_{2}(\gamma ,\beta )\}$ . Assume that $R\geq C(\varepsilon ,X)$ . Lemma 4.4 implies that

(4-4) $$ \begin{align} \|e^{*}\| \geq 1-\gamma, \end{align} $$

and Lemma 4.5 implies the existence of a unit vector $h^{*}\in X^{*}$ satisfying the condition $\|h^{*}-{e^{*}}/{\|e^{*}\|} \| \leq \beta /2$ and a vector $h\in F_{h^{*}}$ such that $|f^{*}(h)|\leq \gamma $ . So $h\in H(e^{*},\beta /2)$ , and since Proposition 2.13 implies $\beta /2<\beta \leq \alpha ({e^{*}}/{\|e^{*}\|},\beta )$ , we have

(4-5) $$ \begin{align} (1-\beta)\|e^{*}\|<e^{*}(h). \end{align} $$

The condition $|f^{*}(h)|\leq \gamma $ implies that

(4-6) $$ \begin{align} e^{*}(h)\leq e^{*}_{1}(h)+\gamma\leq 1+\gamma. \end{align} $$

Conditions (4-4), (4-5) and (4-6) imply

$$ \begin{align*}\|e_{1}^{*}+h^{*}\| &\geq(e_{1}^{*}+h^{*})(h) \geq e^{*}(h)-\gamma +1\\ &\geq (1-\beta)\|e^{*}\| +1-\gamma\geq (1-\beta)(1-\gamma)+1-\gamma.\end{align*} $$

Thus, $\|({e^{*}_{1}+h^{*}})/{2}\|\geq 1-\gamma -\beta \geq \sigma (\varepsilon /2)$ , and therefore, $\| e^{*}_{1}-h^{*}\|\leq \varepsilon /2$ . Conditions (4-4), (4-5) and (4-6) also imply

$$ \begin{align*}1-\gamma\leq \|e^*\|\leq \dfrac{1+\gamma}{1-\beta}.\end{align*} $$

So,

$$ \begin{align*}\|h^{*}-e^{*}\| \leq \bigg\|h^{*}-\dfrac{e^{*}}{\|e^{*}\|}\bigg\|+ |\|e^{*}\|-1|\leq \dfrac{\beta}{2}+\dfrac{\gamma+\beta}{1-\beta} \leq \varepsilon/2.\end{align*} $$

Finally, we get that $\|e^{*}-e_{1}^{*}\|\leq \varepsilon $ , finishing the proof of Lemma 4.3.

In the sequel, we prove Lemmas 4.4, 4.5 and Theorem 1.5.

Proof. Reasoning by contradiction, let us assume that $\|e^{*}\|<1-\gamma $ . Since $f^{*}=e_{1}^{*}-e^{*}$ and $\|e_{1}^{*}\|=\|e_{1}\|=e_{1}^{*}(e_{1})=1$ , we have that $2\geq \|f^{*}\|\ge f^{*}(e_{1})>\gamma $ . Let $y_{0}:=-4\gamma ^{-1}e_{1}$ , and let $y_{1}$ be the point of intersection of $\{te_{1}:t\geq 0\}$ with the line $\{f^{*}=1\}$ . We have $\| y_{1}\|=f^{*}(e_{1})^{-1}<\gamma ^{-1}$ , so

$$ \begin{align*}4\gamma^{-1}<\|y_1-y_0\|<5\gamma^{-1}.\end{align*} $$

Since $R\ge C_{1}:=20\gamma ^{-2}>\| f^{*}\|^{-1}$ , we can apply (H2 $^{\prime }$ ), and we also have $y_{0}\in B_{R}$ and $y_{1}\in B_{R}(y_{0})\subset B_{2R}$ .

For $c\geq 0$ , let $V_{c}$ be the function defined on X by

$$ \begin{align*}V_{c}(x):=e_{1}^{*}(y_{0}) +1+c\|x-y_{0}\|.\end{align*} $$

Notice that, for $c> \|e^{*}\|$ , the set

$$ \begin{align*}E_{c}:=\{x\in X: V_{c}(x)\leq e^{*}(x)\}\end{align*} $$

is convex and compact. We claim that $u(y_{0})\le V_{c}(y_{0})<e^{*}(y_{0})$ . Indeed, $y_{0}\in B_{R}$ , so condition (H1 $^{\prime }$ ) implies the first inequality. On the other hand, $V_{c}(y_{0})=e_{1}^{*}(y_{0})+1=e^{*}(y_{0})+f^{*}(y_{0})+1=e^{*}(y_{0})+1-4f^{*}(e_{1})/\gamma $ , which implies the second inequality.

Let $m:=\max \{c>\|e^{*}\|:E_{c}\cap \partial (\{u<e^{*}\}\cap B_{2R})\neq \emptyset \}$ . The claim implies $y_{0}\in E_{c}$ for every $c>0$ . Since the diameter of $E_{c}$ tends to $0$ as c tends to infinity, we conclude that $E_{c}$ converges to $\{y_{0}\}$ in Hausdorff distance. The claim also implies $u(y_{0})<e^{*}(y_{0})$ , so $m<\infty $ . Now we set

$$ \begin{align*}c_{0}:=1-\dfrac{2}{\|y_{1}-y_{0}\|}> 1-\dfrac{\gamma}{2} >\|e^{*}\|.\end{align*} $$

The equality $\|y_{1}-y_{0}\|=e_{1}^{*}(y_{1}-y_{0})$ implies $V_{c_{0}}(y_{1})=e_{1}^{*}(y_{0})+\|y_{1}-y_{0}\|-1=e_{1}^{*}(y_{1})-f^{*}(y_{1}) =e^{*}(y_{1})$ . Therefore, $y_{1}\in E_{c_{0}}$ , and we know that $y_{0}\in E_{c_{0}}$ , so the segment $[y_{0},y_{1}]$ is included in the convex set $E_{c_{0}}$ . Since $[y_{0},y_{1}]$ crosses the strip $\mathcal {S}$ , it must intersect the polygonal line $\Gamma $ given by (H2 $^{\prime }$ ) which is included in $\{u>e^{*}\}$ . Therefore, $E_{c_{0}}\cap \partial (\{u<e^{*}\}\cap B_{2R})\neq \emptyset $ , which shows that $m\ge c_{0}$ . The compact $E_{m}$ (see Figure 1) is included in the interior of $B_{2R}$ . Indeed, let $x\in E_{m}$ . Since $\|e^{*}\|<1-\gamma $ , we get

Figure 1 Lemma 4.4: The set $E_{m}$ .

$$ \begin{align*}0\le e^*(x)-V_m(x)\le e^*(y_0)-V_m(y_0)+(1-\gamma-m)\|x-y_0\|.\end{align*} $$

Using the inequalities $m> 1-\gamma /2$ and $e^{*}(y_{0})-V_{m}(y_{0})\leq 8/\gamma $ , we obtain $\|x-y_{0}\|<16\gamma ^{-2}$ , and so $\|x\|<20\gamma ^{-2}\leq R$ . Therefore, if $x_{m}\in E_{m}\cap \partial (\{u<e^{*}\}\cap B_{2R})$ , then $\|x_{m}\|<R$ , and so $x_{m}\in \partial \{u<e^{*}\}$ , and by continuity of u, we have that $u(x_{m})=e^{*}(x_{m})$ . Notice now, by definition of m, that we have that $u\leq V_{m}$ in $\partial (E_{m}\setminus \{y_{0}\})$ . Hence, by comparison with cones, $u\leq V_{m}$ in $E_{m}$ . Since $V_{m}$ is an affine function restricted to $[x_{m}, y_{0}]$ and $u(x_{m})=V_{m}(x_{m})\geq V_{m}(y_{0})$ , we get

(4-7) $$ \begin{align} S(x_{m})=-\lim_{r\to 0}\min_{y\in\partial B_{r}(x_{m})}\dfrac{u(y)-u(x_{m})}{r} \geq-\lim_{r\to 0}\dfrac{V_{m}(y_{r})-V_{m}(x_{m})}{r}= m> c_{0}\geq 1-\dfrac{\gamma}{2}, \end{align} $$

where $y_{r}$ is the point of intersection of $\partial B_{r}(x_{m})$ with $[x_{m}, y_{0}]$ . However, we claim that $S(x_{m})\leq \|e^{*}\|+2R^{-1}$ . To this end, let $r>0$ be small and let $U^{\prime }$ be the open set relative to $B_{R}(x_{m})$ defined as the union of all connected components of $\{u>e^{*}\}\cap B_{R}(x_{m})$ that intersect $B_{r}(x_{m})$ . If $U^{\prime }=\emptyset $ , then $u\leq e^{*}$ in $B_{r}(x_{m})$ . Therefore, since $u(x_{m})=e^{*}(x_{m})$ , by Corollary 2.5 we get that $S(x_{m})\leq \|e^{*}\|$ , which proves the claim in this case. If $U^{\prime }\neq \emptyset $ , (H2 $^{\prime }$ ) implies that we have that $U^{\prime }\subset \mathcal {S}$ provided that $r<\mathrm {dist}(x_{m},\Gamma )$ . For ${x\in \partial U^{\prime }\cap \text{int}(B_R)(x_{m})}$ , we have that $u(x)=e^{*}(x)$ . For $x\in U^{\prime }\cap \partial B_{R}(x_{m})$ ,

$$ \begin{align*}u(x)\leq e^{*}(x)+2\leq e^{*}(x_{m})+ R\|e^{*}\|+2,\end{align*} $$

where the first inequality follows as in (4-9), in the proof of Lemma 4.5. Therefore, comparison with cones implies

(4-8) $$ \begin{align} u(x)\leq e^{*}(x_{m})+ (\|e^{*}\|+2R^{-1})\|x-x_{m}\|,\quad\text{for all } x\in U^{\prime} \cap B_{R}(x_{m}). \end{align} $$

Combining (4-8) and the fact that $u\leq e^{*}$ in $B_{r}(x_{m})\setminus U^{\prime }$ , we get that the inequality (4-8) holds in $B_{r}(x_{m})$ . By Corollary 2.5, we conclude that

$$ \begin{align*}S(x_{m})\leq \|e^{*}\|+2R^{-1}.\end{align*} $$

Since $R\geq C_{1}\geq 5\gamma ^{-1}$ , we arrive at $S(x_{m})\leq 1-\gamma /2$ . The last inequality contradicts (4-7), finishing the proof of Lemma 4.4.

Proof of Lemma 4.5

If $\|f^{*}\|\leq \gamma $ , the conclusion is direct. For this, let us assume that $\|f^{*}\|>\gamma $ . If we further assume that $C_{2}\geq 3/\gamma $ , since $R\geq C_{2}$ , the conclusion of hypothesis $(H^{\prime }_{2})$ is available for us. Reasoning by contradiction, we have

$$ \begin{align*} \inf \bigg\{|f^{*}(h)|:h\in H\bigg(e^{*},\dfrac{\beta}{2}\bigg) \bigg\}\geq \gamma. \end{align*} $$

Let e be a unit vector in X such that $e^{*}(e)=\|e^{*}\|$ , and let $x_{0}$ be the point of intersection of $\partial \mathcal {S}$ with the half line $\{-te:t>0\}$ . See Figure 2. We have that $x_{0}=-t_{0}e$ , where $t_{0}$ satisfies

$$ \begin{align*}1=t_{0}|f^{*}(e)|\geq t_{0}\gamma. \end{align*} $$

So, $\|x_{0}\|=t_{0}\leq 1/\gamma \leq C_{2}\leq R$ . Thus $-x_{0}\in B_{R}(x_{0})\subset B_{2R}$ . Hypotheses (H1 $^{\prime }$ ) and (H2 $^{\prime }$ ) imply

$$ \begin{align*} |u(x)-e^{*}(x)|\leq |u(x)-e^{*}_{1}(x)|+|e^{*}(x)-e_{1}^{*}(x)|\leq 2,& \quad\text{for all }x\in \mathcal{U}\cap B_{R}(x_{0}). \\ u(x)=e^{*}(x)& \quad\text{for all } x\in \partial \mathcal{U}\cap B_{R}(x_{0}). \end{align*} $$

Hence, if $x\in \mathcal {U}\cap \partial B_{R}(x_{0})$ , then

(4-9) $$ \begin{align} u(x)\leq e^{*}(x)+2\leq e^{*}(x_{0})+\sup_{x\in \mathcal{S}\cap \partial B_{R}(x_{0})} e^{*}(x-x_{0})+2. \end{align} $$

Figure 2 Lemma 4.5: Ball of radius R centered at $x_{0}$ .

Since $R\geq C_{2}$ , $|f^{*}(Rh)|\geq 3$ for every $h\in H(e^{*},\beta /2)$ . Therefore, $|f^{*}(Rh-x_{0})|\geq 2>1$ for every $h\in H(e^{*},\beta /2)$ , that is,

$$ \begin{align*}(\mathcal{S}\cap \partial B_{R}(x_{0}) )\cap (RH(e^{*},\beta/2)-x_{0}) = \emptyset.\end{align*} $$

By Proposition 2.14, with $\sigma =\beta /2$ , we obtain $\rho \in (0,1)$ depending on $\beta $ , such that

(4-10) $$ \begin{align} e^{*}(x-x_{0})\leq(1-\rho)\|e^{*}\|\, \|x-x_{0}\|, \quad\text{for all }x\in \mathcal{S}\cap \partial B_{R}(x_{0}). \end{align} $$

Let us assume now that $C_{2}\geq {3}/{(\gamma \rho )}> {3}/{\gamma }$ . Since $R\geq C_{2}$ and $\|e^{*}\|\geq \gamma $ , we get $ R\|e^{*}\|\rho \geq 2$ . Combining (4-9) and (4-10), we get

$$ \begin{align*}u(x)\leq e^{*}(x_{0})+\|e^{*}\|\,\|x-x_{0}\|, \quad\text{for all }x\in \mathcal{U}\cap \partial B_{R}(x_{0}).\end{align*} $$

From comparison with cones, we obtain

$$ \begin{align*}u(x)\leq e^{*}(x_{0})+\|e^{*}\|\,\|x-x_{0}\|,\quad\text{for all }x\in \mathcal{U}\cap B_{R}(x_{0}). \end{align*} $$

In particular,

$$ \begin{align*}u(x)\leq e^{*}(x),\quad\text{for all }x\in \mathcal{U}\cap B_{R}(x_{0})\cap \{x_{0}+te:t>0\}. \end{align*} $$

This is a contradiction with $(H_{2}^{\prime })$ since $\mathcal {U}\cap B_{R}(x_{0})\cap \{x_{0}+te:t>0\}$ necessarily intersects $\Gamma $ .□

We are now in a position to present the proof of Theorem 1.5.

Proof of Theorem 1.5

If $\|e_{1}^{*}\|=0$ , there is nothing to prove. If $\|e_{1}^{*}\|\ne 0$ , by homogeneity, we can assume $\|e_{1}^{*}\|=1$ . By Theorem 1.3, there exists $(e^{*}_{0,r})_{r}\subset X^{*}$ such that $\|e^{*}_{0,r}\|=S(0)$ for every r and

(4-11) $$ \begin{align} |u(x)-u(0)-e_{0,r}^{*}(x)|\leq r\sigma(r),\quad\text{for all }x\in B_{r}, \end{align} $$

where $\sigma :\mathbb {R}_{+}\to \mathbb {R}$ is a positive function such that $\sigma (r)$ tends to $0$ as r tends to $0$ .

Let us fix $\varepsilon>0$ . We need to find $\delta :=\delta (\varepsilon )>0$ such that, if $|u(x)-e_{1}^{*}(x)|\leq \delta $ in $\text {int}(B_{1})$ , then

(4-12) $$ \begin{align} \limsup_{r\to 0}\|e_{0,r}^{*}-e_{1}^{*}\|\leq \varepsilon. \end{align} $$

First case. Suppose that u is not identical to an affine function in any neighborhood of $0$ . We show that if $\delta \leq \delta _{1}(\varepsilon )=\min \{\lambda (\varepsilon /4)/4, 1/2\}$ , where $\lambda $ is the function given in Proposition 4.2, then (4-12) holds. Let $r\in (0,1/2)$ be such that $\sigma (r)\le \lambda (\varepsilon /4)S(0)/4$ . Thanks to Proposition 4.1, replacing u by $-u$ if necessary, there exist $y\in \text {int}(B_{r/24})$ and a linear form $e^{*}\in X^{*}$ satisfying $\| e^{*}\|=S(y)$ , such that the set

$$ \begin{align*}\mathcal{O}=\{u>e^{*}+u(y)-e^{*}(y)\}\cap \text{ int }(B_{1})\end{align*} $$

has at least two distinct connected components intersecting $\text {int}(B_{r/24})$ . The function $v(\cdot ):=u(\cdot +y)-u(y)$ is well defined on int $(B_{1/2})$ . Let us check that v satisfies the hypotheses of Proposition 4.2. The set $\{v>e^{*}\}=(\mathcal {O}-y)\cap \text {int}(B_{1/2})$ has at least two distinct connected components intersecting $B_{r/12}\subset B_{1/12}$ . On the other hand, for $x\in B_{1/2}$ we have

$$ \begin{align*}|v(x)-e_{1}^{*}(x)|\leq |u(x+y)-e^{*}_{1}(x+y)|+|u(y)-e^{*}_{1}(y)|\leq 2\delta.\end{align*} $$

Since $2\delta \le \lambda (\varepsilon /4)/2$ , thanks to Proposition 4.2 applied with $\rho =1/2$ , we get

(4-13) $$ \begin{align} \|e^{*}-e^{*}_{1}\|\leq \dfrac{\varepsilon}{4}. \end{align} $$

Since $|u(x)-e^{*}_{1}(x)|\leq \delta $ in $\text {int}(B_{1})$ and $\|e_{1}^{*}\|=1$ , we obtain

$$ \begin{align*} \|e^{*}_{0,r}\|=S(0)\leq S^{+}\big(0,\tfrac{1}{2}\big)= 2\max_{x\in \partial B_{1/2}} {u(x)-u(0)}\leq 1+4\delta. \end{align*} $$

We now apply Proposition 4.2 to the function v on $B_{r/2}$ . The set $\{v>e^{*}\}\cap \text {int}(B_{r/2})$ has at least two distinct connected components that intersect $B_{r/12}$ . On the other hand, thanks to (4-11), for $x\in B_{r/2}$ we have that

$$ \begin{align*} |v(x)-e_{0,r}^{*}(x)|\leq |u(x+y)-u(0)-e_{0,r}^{*}(x+y)|+ |u(y)-u(0)-e_{0,r}^{*}(y)|\leq 2r\sigma(r). \end{align*} $$

Since $2\sigma (r)\le \lambda (\varepsilon /4)\|e_{0,r}^{*}\|/2$ , we get that

$$ \begin{align*}|v(x)-e_{0,r}^{*}(x)|\leq \dfrac{r}{2}\lambda(\varepsilon/4)\|e_{0,r}^{*}\|,\quad\text{for all }x\in B_{r/2}.\end{align*} $$

Finally, we can apply Proposition 4.2 with $\rho =r/2$ to obtain

(4-14) $$ \begin{align} \|e^{*}-e_{0,r}^{*}\|\leq\dfrac{\varepsilon\|e_{0,r}^{*}\|}{4}\leq\dfrac{(1+4\delta)\varepsilon}{4}\leq\dfrac{3\varepsilon}{4}. \end{align} $$

Combining (4-13) with (4-14), we get that $\|e_{1}^{*}-e_{0,r}^{*}\| \leq \varepsilon $ . Thus (4-12) is satisfied in this case whenever $\delta \le \delta _{1}(\varepsilon )$ .

Second case. Suppose that there exists $e_{0}^{*}\in X^{*}$ such that $u=e_{0}^{*}$ in a neighborhood of $0$ . Let

$$ \begin{align*}R=\max\{r\in(0,1];\,\{u=e_{0}^{*}\}\subset B_{r}\}.\end{align*} $$

If $R\ge 1/2$ , notice that $e_{0,r}^{*}=e_{0}^{*}$ satisfies (4-11) whenever $r\leq 1/2$ . Assume $\delta \le \varepsilon /2$ and $|u(x)-e^{*}_{1}(x)|<\delta $ in $\text {int}(B_{1})$ . Since $u=e_{0}^{*}$ in $B_{1/2}$ , we get $\limsup _{r\to 0}\|e_{0,r}^{*}-e_{1}^{*}\|=\|e_{0}^{*}-e_{1}^{*}\|\leq \varepsilon $ .

If $R< 1/2$ , there exists $x_{0}\in \partial B_{R}$ such that u is not identical to an affine function in any neighborhood of $x_{0}$ . Let us define the AML function $v:B_{1}\to \mathbb {R}$ by

$$ \begin{align*}v(\cdot):= u\bigg(\dfrac{\cdot}{2}+x_{0}\bigg)-u(x_{0}).\end{align*} $$

Since v is not affine in any neighborhood of $0$ , we wish to apply the first case to the function v. According to Theorem 1.3, there exists $(e^{*}_{x_{0},r})_{r}\subset X^{*}$ such that $\|e^{*}_{0,r}\|=S(x_{0})$ for every $r\in (0,1)$ and

$$ \begin{align*}|u(x)-u(x_{0})-e_{x_{0},r}^{*}(x-x_{0})|\leq r\widetilde{\sigma}(r),\quad\text{for all }x\in B_{r}(x_{0}),\end{align*} $$

where $\widetilde {\sigma }:\mathbb {R}_{+}\to \mathbb {R}$ is a positive function such that $\widetilde {\sigma }(r)$ tends to $0$ as r tends to $0$ . So, for $r\in (0,1/2)$ , we have

(4-15) $$ \begin{align} \bigg|v(x)-v(0)-\dfrac{e_{x_{0},r}^{*}}{2}(x)\bigg|=\bigg|u\bigg(\dfrac{x}{2}+x_{0}\bigg)-u(x_{0}) -e_{x_{0},r}^{*}\bigg(\dfrac{x}{2}\bigg)\bigg|\leq r\widetilde{\sigma}(r),\quad\text{for all }x\in B_{r}. \end{align} $$

Let us suppose that $\delta \le \delta _{1}(\varepsilon /2)/2$ . Since $|u(x)-e_{1}^{*}(x)|\leq \delta $ in $\text {int}(B_{1})$ , we have, for every $x\in B_{1}$ ,

(4-16) $$ \begin{align} \bigg|v(x)-\dfrac{e_{1}^{*}}{2}(x)\bigg|\leq \bigg|u\bigg(\dfrac{x}{2}+x_{0}\bigg)-e_{1}^{*}\bigg(\dfrac{x}{2}+x_{0}\bigg)\bigg|+|u(x_{0})-e_{1}^{*}(x_{0})|\leq \delta_{1}\bigg(\frac{\varepsilon}{2}\bigg). \end{align} $$

Let us check that $S_{v}(0)>0$ . We know that $\|e_{0}^{*}\|=S_{u}(0)\ne 0$ . Since $\|x_{0}\|=R$ and $u=e_{0}^{*}$ on $B_{R}$ , we can apply Corollary 2.4 to get

$$ \begin{align*}S_{v}(0)=\dfrac{S_{u}(x_{0})}{2}>0. \end{align*} $$

Conditions (4-15) and (4-16) allow us to apply the first case to v. We get

(4-17) $$ \begin{align} \limsup_{r\to 0}\bigg\| \dfrac{e_{1}^{*}}{2}-\dfrac{e_{x_{0},r}^{*}}{2} \bigg\|\leq \dfrac{\varepsilon}{2}. \end{align} $$

Let us now show that $e^{*}_{x_{0},r}$ tends to $e_{0}^{*}$ as r tends to $0$ . Reasoning by contradiction, assume that there exists a null sequence $(r_{i})_{i}$ such that $e_{x_{0},r_{i}}^{*}$ converges to some $h^{*}\neq e_{0}^{*}$ . So, there exist $z\in \partial B_{1}$ and $t>0$ such that the open segment $(x_{0},x_{0}+t z)$ is included in U and ${(e_{0}^{*}-h^{*})(z)\neq 0}$ . Finally, we compute

$$ \begin{align*}\lim_{i\to\infty}\dfrac{u(x_{0}+r_{i}z)-u(x_{0})}{r_{i}}-e_{x_{0},r_{i}}^{*}(z)=e_{0}^{*}(z)-h^{*}(z) \neq 0, \end{align*} $$

which contradicts Theorem 1.3. Hence, $e_{x_{0},r}^{*}$ converges to $e_{0}^{*}$ , and from (4-17) we get

$$ \begin{align*}\limsup_{r\to 0} \|e_{0,r}^{*}-e_{1}^{*} \|=\|e_{0}^{*}-e_{1}^{*} \| = \limsup_{r\to 0} \|e^{*}_{x_{0},r}-e_{1}^{*} \|\leq \varepsilon.\end{align*} $$

Thus, (4-12) is satisfied whenever

$$ \begin{align*}\delta (\epsilon )=\min \{\delta _{1}(\varepsilon /2)/2,\varepsilon /2\}=\min \{\lambda (\varepsilon /8)/8, 1/4, \varepsilon /2\}.\end{align*} $$

This completes the proof of Theorem 1.5.