Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T12:33:58.794Z Has data issue: false hasContentIssue false
  • English
  • Français

REAL ZEROS OF ALGEBRAIC POLYNOMIALS WITH STABLE RANDOM COEFFICIENTS

Part of: Stochastic processes

Published online by Cambridge University Press:  01 August 2008

K. FARAHMAND
K. FARAHMAND*
Affiliation:
Department of Mathematics, University of Ulster at Jordanstown, Country Antrim, BT37 0QB, United Kingdom (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Weconsider a random algebraic polynomial of the form Pn,θ,α(t)=θ0ξ0+θ1ξ1t+⋯+θnξntn, where ξk, k=0,1,2,…,n have identical symmetric stable distribution with index α, 0<α≤2. First, for a general form of θk,α≡θk we derive the expected number of real zeros of Pn,θ,α(t). We then show that our results can be used for special choices of θk. In particular, we obtain the above expected number of zeros when 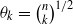. The latter generate a polynomial with binomial elements which has recently been of significant interest and has previously been studied only for Gaussian distributed coefficients. We see the effect of α on increasing the expected number of zeros compared with the special case of Gaussian coefficients.

Keywords

random polynomialsnumber of real zerosreal rootsKac–Rice formulastable random variables

MSC classification

Secondary: 60G99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 1 , August 2008 , pp. 81 - 86
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Bharucha-Reid, A. T. and Sambandham, M., Random Polynomials (Academic Press, New York, 1986).Google Scholar
[2]Edelman, A. and Kostlan, E., ‘How many zeros of a random polynomial are real?’, Bull. Amer. Math. Soc. 32 (1995), 1–37.CrossRefGoogle Scholar
[3]Farahmand, K., Topics in Random Polynomials (Longman, London, 1998).Google Scholar
[4]Farahmand, K. and Nezakati, A., ‘Algebraic polynomials with non-identical random coefficients’, Proc. Amer. Math. Soc. 133 (2005), 275–283.CrossRefGoogle Scholar
[5]Kac, M., ‘On the average number of real roots of a random algebraic equation’, Bull. Amer. Math. Soc. 49 (1943), 314–320.CrossRefGoogle Scholar
[6]Logan, B. F. and Shepp, L. A., ‘Real zeros of random polynomials’, Proc. London Math. Soc. 18 (1968), 29–35.Google Scholar
[7]Logan, B. F. and Shepp, L. A., ‘Real zeros of random polynomials. II’, Proc. London Math. Soc. 18 (1968), 308–314.Google Scholar
[8]Ramponi, A., ‘A note on the complex roots of complex random polynomials’, Stat. Probab. Lett. 44 (1999), 181–187.Google Scholar
[9]Wilkins, J. E., ‘An asymptotic expansion for the expected number of real zeros of a random polynomial’, Proc. Amer. Math. Soc. 103 (1988), 1249–1258.Google Scholar
[10]Wilkins, J. E., ‘Mean number of real zeros of a random trigonometric polynomial’, Proc. Amer. Math. Soc. 111 (1991), 851–863.Google Scholar