Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T08:25:33.670Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational approximation with series

Published online by Cambridge University Press:  09 April 2009

D. Fenna
D. Fenna
Affiliation:
Department of Defence, Canberra.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Siegel conjecture on the rational approximation to algebraic numbers was proved a few years ago by K. F. Roth [1] with the following theorem: Let α be any algebraic number, not rational. If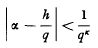 has an infinity of solutions in integers h and q (q > 0) tehn k ≤ 2.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 2 , Issue 1 , April 1961 , pp. 107 - 119
Copyright
Copyright © Australian Mathematical Society 1961

References

[1]Roth, K. F., Rational approximations to algebraic numbers. Mathematika, Vol. 2, p. 1.CrossRefGoogle Scholar
[2]Gill, B. P., An analogue for algebraic functions of the Thue-Siegel theorem. Annals of Maths., Ser. 2, Vol. 31, p. 207.CrossRefGoogle Scholar
[3]Mahler, K., On a theorem of Liouville in fields of positive characteristic. Canadian Journal of Maths., Vol. 1, p. 397.CrossRefGoogle Scholar