Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T07:17:37.861Z Has data issue: false hasContentIssue false
  • English
  • Français

Radius of univalence and starlikeness of a class of analytic functions

Published online by Cambridge University Press:  09 April 2009

R. S. Gupta
R. S. Gupta
Affiliation:
Department of Mathematics, Punjabi UniversityPatiala, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Letp denote the family of functions 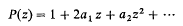regular in E{z:|z| < 1} and with positive real part there. We propose to study, in this article, the subclass p2a1 of p whose functions P(z) have pre-assigned second coefficient 2a1. In what follows we may assume, without loss in generality, that a1 is real and non-negative. This assumption will be made throughout. As is well known [2], 0 ≦ a1 ≦ 1. In Theorem 1 we derive a generalization of Zmorovic's theorem 1, [3]. determine the radius of univalence and starlikeness of the class of functions

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 14 , Issue 1 , July 1972 , pp. 1 - 8
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Landau, E., ‘Der Picard-Schottkysche Satz un die Blochsche Konstante’, Sitzungsb. Akad. d. Wiss. Berlin, Phys. Math. Klasse (1926), 467–474.Google Scholar
[2]Nehari, Z., Conformal Mapping (McGraw-Hill, 1952).Google Scholar
[3]Zmorovic, V. A., ‘On the radius of convexity of starlike functions of order a regular in |z| < 1 and in 0 < |z| < 1’ (Russian), Mat. Sbornik (N. S.) 68 (110) (1965), 518–526.Google Scholar