Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T08:43:10.401Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASICONVEXITY OF BANDS IN HYPERBOLIC 3-MANIFOLDS

Part of: Low-dimensional topology

Published online by Cambridge University Press:  01 April 2014

BRIAN H. BOWDITCH
BRIAN H. BOWDITCH*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 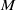$M$ be a complete hyperbolic 3-manifold homotopy equivalent to a compact surface 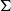$\Sigma $. Let 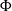$\Phi $ be a proper subsurface of 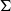$\Sigma $, whose boundary is sufficiently short in 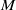$M$. We show that the union of all Margulis tubes and cusps homotopic into 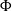$\Phi $ lifts to a uniformly quasiconvex subset of hyperbolic 3-space.

Keywords

hyperbolic 3-manifoldsurface groupquasiconvexity

MSC classification

Secondary: 57M50: Geometric structures on low-dimensional manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 2 , April 2014 , pp. 167 - 185
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Agol, I., ‘Tameness of hyperbolic 3-manifolds’, Preprint, Chicago, IL, 2004, available at arXiv:0405.5568.Google Scholar
Bonahon, F., ‘Bouts des variétés hyperboliques de dimension 3’, Ann. of Math. (2) 124 (1986), 71–158.Google Scholar
Bowditch, B. H., ‘Systems of bands in hyperbolic 3-manifolds’, Pacific J. Math. 232 (2007).CrossRefGoogle Scholar
Bowditch, B. H., ‘Atoroidal surface bundles over surfaces’, Geom. Funct. Anal. 19 (2009), 943–988.Google Scholar
Bowditch, B. H., The ending lamination theorem, available at http://homepages.warwick.ac.uk/~masgak/papers/elt.pdf.Google Scholar
Bowditch, B. H., ‘An upper bound for injectivity radii in convex cores’, Groups Geom. Dyn. 7 (2013), 109–136.Google Scholar
Brock, J. F., Canary, R. D. and Minsky, Y. N., ‘Classification of Kleinian surface groups II: The ending lamination conjecture’, Ann. of Math. (2) 176 (2012), 1–149.Google Scholar
Calegari, D. and Gabai, D., ‘Shrinkwrapping and the taming of hyperbolic 3-manifolds’, J. Amer. Math. Soc. 19 (2006), 385–446.Google Scholar
Canary, R. D., ‘A covering theorem for hyperbolic 3-manifolds and its applications’, Topology 35 (1996), 751–778.Google Scholar
Epstein, D. B. A. and Marden, A., ‘Convex hulls in hyperbolic space, a theorem of Sullivan, and measured pleated surfaces’, in: Analytic and Geometric Aspects of Hyperbolic Space, London Mathematical Society Lecture Notes Series, 111 (Cambridge University Press, Cambridge, 1987), 113–253.Google Scholar
Hatcher, A. E. and Thurston, W. P., ‘A presentation for the mapping class group of a closed orientable surface’, Topology 19 (1980), 221–237.Google Scholar
Hempel, J., 3-manifolds, Ann. of Mathematical Studies, 86 (Princeton University Press, Princeton, NJ, 1976).Google Scholar
Minsky, Y. N., ‘The classification of Kleinian surface groups I: Models and bounds’, Ann. of Math. (2) 171 (2010), 1–107.Google Scholar
Mj, M., ‘Cannon–Thurston maps for surface groups I: Amalgamation geometry and split geometry’, Preprint, Belur Math, 2006.Google Scholar
Mj, M., ‘Cannon–Thurston maps for surface groups II: Split geometry and the Minsky model’, Preprint, Belur Math, 2010.Google Scholar
Ohshika, K. and Soma, T., ‘Geometry and topology of geometric limits I’, Preprint, Osaka/Tokyo, 2010, available at arXiv:1002.4266.Google Scholar
Otal, J.-P., ‘Les géodésiques fermées d’une variété hyperbolique en tant que noeuds’, in: Kleinian Groups and Hyperbolic 3-Manifolds, London Mathematical Society Lecture Notes Series, 299 (eds. Komori, Y., Markovic, V. and Series, C.) (Cambridge University Press, Cambrige, 2003), 95–104.Google Scholar
Thurston, W. P., ‘The geometry and topology of 3-manifolds’, manuscript, Princeton, 1979, available at http://library.msri.org/books/gt3m.Google Scholar