Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-29T11:31:30.177Z Has data issue: false hasContentIssue false
  • English
  • Français

The product of independent random variables with slowly varying truncated moments

Part of: Limit theorems Distribution theory - Probability

Published online by Cambridge University Press:  09 April 2009

Takaaki Shimura
Takaaki Shimura
Affiliation:
The Institute of Statistical Mathematics4-6-7 Minami-Azabu Minato-Ku Tokyo 106Japan e-mail: [email protected]. jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Mellin-Stieltjes convolution and related decomposition of distributions in M(α) (the class of distributions μ on (0, ∞) with slowly varying αth truncated moments 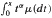) are investigated. Maller shows that if X and Y are independent non-negative random variables with distributions μ and v, respectively, and both μ and v are in D2, the domain attraction of Gaussian distribution, then the distribution of the product XY (that is, the Mellin-Stieltjes convolution μ ^ v of μ and v) also belongs to it. He conjectures that, conversely, if μ ∘ v belongs to D2, then both μ and v are in it. It is shown that this conjecture is not true: there exist distributions μ ∈ D2 and v μ ∈ D2 such that μ ^ v belongs to D2. Some subclasses of D2 are given with the property that if μ ^ v belongs to it, then both μ and v are in D2.

Keywords

domain of attractiontruncated momentslowly varying functionregular variationMellin-Stieltjes convolution

MSC classification

Secondary: 60E05: Distributions 60E07: Infinitely divisible distributions; stable distributions 60F05: Central limit and other weak theorems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 62 , Issue 2 , April 1997 , pp. 186 - 197
Copyright
Copyright © Australian Mathematical Society 1997

References

[1]Bingham, N. M., Goldie, C. M. and Teugels, J. L., Regular variation, Encyclopedia Math. Appl. (Cambridge University Press, Cambridge, 1987).CrossRefGoogle Scholar
[2]Feller, W., An introduction to probability theory and its applications, volume II, second edition (Willey, New York, 1971).Google Scholar
[3]Gnedenko, B. V. and Kolmogorov, A. N., Limit distributions for sums of independent random variables, second edition (Addison Wesley, Cambridge, 1968).Google Scholar
[4]Maller, R. A., ‘A note on domain of partial attraction’, Ann. Probab. 3 (1980), 576–583.Google Scholar
[5]Maller, R. A., ‘A theorem on products of random variables, with application to regression’, Austral. J. Statist. 23 (1981), 177–185.CrossRefGoogle Scholar
[6]Seneta, E., Regularly varying functions, Lecture Notes in Math. 508 (Springer, Berlin, 1976).Google Scholar
[7]Shimura, T., ‘Decomposition of non-decreasing slowly varying functions and the domain of attraction of Gaussian distributions’, J. Math. Soc. Japan 43 (1991), 775–793.Google Scholar
[8]Shimura, T., ‘Decomposition of probability measures related to monotone regularly varying functions’, Nagoya Math. J. 135 (1994), 87–111.Google Scholar