Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T08:45:43.943Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIMITIVE PRIME DIVISORS AND THE $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL

Part of: Computational number theory Linear algebraic groups and related topics Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  04 November 2015

S. P. GLASBY ,
FRANK LÜBECK ,
ALICE C. NIEMEYER  and
CHERYL E. PRAEGER
S. P. GLASBY
Affiliation:
Centre for Mathematics of Symmetry and Computation, University of Western Australia, Australia The Department of Mathematics, University of Canberra, Australia email [email protected]
FRANK LÜBECK
Affiliation:
Lehrstuhl D für Mathematik, RWTH Aachen University, Pontdriesch 14/16, 52062 Aachen, Germany email [email protected]
ALICE C. NIEMEYER*
Affiliation:
Lehr- und Forschungsgebiet Algebra, RWTH Aachen University, Pontdriesch 10-16, 52062 Aachen, Germany email [email protected]
CHERYL E. PRAEGER
Affiliation:
Centre for Mathematics of Symmetry and Computation, University of Western Australia, Australia King Abdulaziz University, Jeddah, Saudi Arabia email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Primitive prime divisors play an important role in group theory and number theory. We study a certain number-theoretic quantity, called 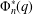$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ , which is closely related to the cyclotomic polynomial 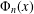$\unicode[STIX]{x1D6F7}_{n}(x)$ and to primitive prime divisors of 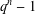$q^{n}-1$ . Our definition of 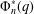$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)$ is novel, and we prove it is equivalent to the definition given by Hering. Given positive constants $c$ and 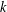$k$ , we provide an algorithm for determining all pairs 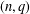$(n,q)$ with 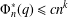$\unicode[STIX]{x1D6F7}_{n}^{\ast }(q)\leq cn^{k}$ . This algorithm is used to extend (and correct) a result of Hering and is useful for classifying certain families of subgroups of finite linear groups.

Keywords

Zsigmondy primescyclotomic polynomial

MSC classification

Primary: 11T22: Cyclotomy
Secondary: 11Y40: Algebraic number theory computations 20G05: Representation theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 1 , February 2017 , pp. 122 - 135
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bamberg, J. and Penttila, T., ‘Overgroups of cyclic sylow subgroups of linear groups’, Comm. Algebra 36 (2008), 2503–2543.Google Scholar
Bang, A. S., ‘Taltheoretiske Undersøgelser’, Tidsskr. Math. (5) 4 (1886), 70–80; and 130–137.Google Scholar
Biliotti, M., Jha, V., Johnson, N. L. and Montinaro, A., ‘Translation planes of order q 2 admitting a two-transitive orbit of length q + 1 on the line at infinity’, Des. Codes Cryptogr. 44 (2007), 69–86.CrossRefGoogle Scholar
Biliotti, M., Jha, V., Johnson, N. L. and Montinaro, A., ‘Two-transitive groups on a hyperbolic unital’, J. Combin. Theory Ser. A 115 (2008), 526–533.Google Scholar
Biliotti, M., Jha, V., Johnson, N. L. and Montinaro, A., ‘Classification of projective translation planes of order q 2 admitting a two-transitive orbit of length q + 1’, J. Geom. 90(1–2) (2008), 100–140.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.Google Scholar
Camina, A. R. and Whelan, E. A., Linear Groups and Permutations, Research Notes in Mathematics, 118 (Pitman (Advanced Publishing Program), Boston, MA, 1985).Google Scholar
Dandapat, G. G., Hunsucker, J. L. and Pomerance, C., ‘Some new results on odd perfect numbers’, Pacific J. Math. 57 (1975), 359–364.Google Scholar
DiMuro, J., ‘On prime power order elements of general linear groups’, J. Algebra 367 (2012), 222–236.Google Scholar
Dummit, D. S. and Foote, R. M., Abstract Algebra, 3rd edn, (Wiley & Sons, Hoboken, 2004).Google Scholar
Feit, W., ‘On large Zsigmondy primes’, Proc. Amer. Math. Soc. 102 (1988), 29–36.Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, version 4.7.7; 2015,http://www.gap-system.org.Google Scholar
Glasby, S. P., Supporting GAP and Magma code, http://www.maths.uwa.edu.au/∼glasby/RESEARCH.Google Scholar
Guralnick, R., Penttila, T., Praeger, C. E. and Saxl, J., ‘Linear groups with orders having certain large prime divisors’, Proc. Lond. Math. Soc. 78 (1999), 167–214.Google Scholar
Hering, C., ‘Transitive linear groups and linear groups which contain irreducible subgroups of prime order’, Geom. Dedicata 2 (1974), 425–460.Google Scholar
James, G. D., ‘On the minimal dimensions of irreducible representations of symmetric groups’, Math. Proc. Cambridge Philos. Soc. 94 (1983), 417–424.Google Scholar
Lenstra–Pomerance–Wagstaff conjecture, http://primes.utm.edu/mersenne/heuristic.html.Google Scholar
Lüneburg, H., ‘Ein einfacher Beweis für den Satz von Zsigmondy über primitive Primteiler von A N - 1. [A simple proof of Zsigmondy’s theorem on primitive prime divisors of A N - 1]’, in: Geometries and Groups (Springer, Berlin, 1981), 219–222.Google Scholar
Niemeyer, A. C. and Praeger, C. E., ‘A recognition algorithm for classical groups over finite fields’, Proc. Lond. Math. Soc. 77 (1998), 117–169.Google Scholar
Ribenboim, P., The Little Book of Big Primes (Springer, New York, 1991).Google Scholar
Roitman, M., ‘On Zsigmondy primes’, Proc. Amer. Math. Soc. 125 (1997), 1913–1919.CrossRefGoogle Scholar
Zsigmondy, K., ‘Zur Theorie der Potenzreste’, Monatsh. Math. 3 (1892), 265–284.Google Scholar