Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T09:20:03.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial solutions of binomial congruences

Published online by Cambridge University Press:  09 April 2009

H. Lindgren
H. Lindgren
Affiliation:
Patent Office, Canberra.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Polynomial solutions of a few binomial congruences have been known for a long time. For instance Legendre showed that the congruence 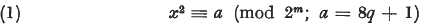has a solution 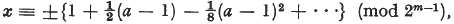this being the expansion of 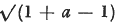as far as the term of degree m — 3. [1] It seems that only restricted types, e.g. (1), have been investigated.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 1 , Issue 3 , August 1960 , pp. 257 - 280
Copyright
Copyright © Australian Mathematical Society 1960

References

[1]Proved in Uspensky, J. V. and Heaslet, M. A., Elementary Number Theory, pp. 311–4.Google Scholar
For further polynomial and other explict solutions see Dickson, L. E., History of the Theory of Numbers, vol. 1, ch. VII.Google Scholar
[2]Nagell, T., Introduction to Number Theory, p. 118, Theorem 71.Google Scholar
[3]Uspensky, and Heaslet, , Elementary Number Theory, p. 103, ex. 1. Proved in Griffin H., Elementary Theory of Numbers, pp. 42–3.Google Scholar
[4]Fort, T., Finite Differences, p. 10, Theorem IV.Google Scholar
[5]Nagell, , Introduction to Number Theory, p. 104, Theorem 63.Google Scholar
[6]Cipolla, M. obtained (51) for a quadratic congruence in the following form. The solution of where (In (15) let on the right.) He later extended the exponent of x to any divisor of p — 1 (i.e. n=d and m = 1 in the notation used here), and found an equivalent of (50) for this case.Google Scholar
(Dickson's History, vol. 1, pp. 219, 220;Google Scholar
Rendiconto Accad. Sc. Fis. e Mat. Napoli (3), 11 (1905), 13–19;Google Scholar
Math. Annalen, 63 (1907), 54–61.)Google Scholar