Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Horadam, K. J.
2010.
Hadamard matrices and their applications: Progress 2007–2010.
Cryptography and Communications,
Vol. 2,
Issue. 2,
p.
129.


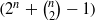 -dimensional GF(2
-dimensional GF(2