Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:37:02.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Polyhedral convex cones and the equational theory of the bicyclic semigroup

Part of: Semigroups

Published online by Cambridge University Press:  09 April 2009

F. Pastijn
F. Pastijn
Affiliation:
Department of Mathematics, Statistics and Computer Science, Marquette University, Milwaukee WI 53201-1881, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To any given balanced semigroup identity U ≈ W a number of polyhedral convex cones are associated. In this setting an algorithm is proposed which determines whether the given identity is satisfied in the bicylic semigroup 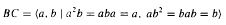or in the semigroup 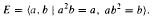. The semigroups BC and E deserve our attention because a semigroup variety contains a simple semigroup which is not completely simple (respectively, which is idempotent free) if and only if this variety contains BC (respectively, E). Therefore, for a given identity U ≈ W it is decidable whether or not the variety determined by U ≈ W contains a simple semigroup which is not completely simple (respectively, which is idempotent free).

MSC classification

Secondary: 20M05: Free semigroups, generators and relations, word problems 20M07: Varieties and pseudovarieties of semigroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 81 , Issue 1 , August 2006 , pp. 63 - 96
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Adjan, S. I., Defining relations and algorithmic problems for groups and semigroups, Proceedings of the Steklov Institute of Mathematics 85. Translated from Russian by M. Greendlinger (Amer. Math. Soc., Providence, 1967).Google Scholar
[2]Aizenstat, A. Ya., ‘On covers in the lattice of semigroup varieties’, in: Contemporary calculus and geometry (ed. Bakel'man, I. Ya.), Collection of Scientific Works (Leningrad State Pedagogical Institute, 1972) pp. 3–11 (in Russian).Google Scholar
[3]Andersen, O., Ein Bericht über die Struktur abstrakter Halbgruppen (Staatsexamensarbeit, Hamburg, 1952).Google Scholar
[4]Byleen, K., ‘Embedding any countable semigroup in a 2-generated bisimple monoid’, Glasgow Math. J. 25 (1984), 153–161.CrossRefGoogle Scholar
[5]Byleen, K., ‘Embedding any countable semigroup without idempotents in a 2-generated simple semigroup without idempotents’, Glasgow Math. J. 30 (1988), 121–128.CrossRefGoogle Scholar
[6]Byleen, K., ‘Embedding any countable semigroup in a 2-generated congruence-free semigroup’, Semigroup Forum 41 (1990), 145–153.CrossRefGoogle Scholar
[7]Carver, W. B., ‘Systems of linear inequalities’, Ann. of Math. (2) 23 (1922), 212–220.CrossRefGoogle Scholar
[8]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Math. Surveys 7 (Amer. Math. Soc., Providence, 1961 (Vol. I) and 1967 (Vol. II)).Google Scholar
[9]Fan, K., ‘On systems of Linear inequalities’, in: Linear inequalities and related systems (eds. Kuhn, H. W. and Tucker, A. W.), Annals of Mathematics Studies 38 (Princeton University Press, Princeton, 1956) pp. 99–156.Google Scholar
[10]Goldman, A. J. and Tucker, A. W., ‘Polyhedral convex cones’, in: Linear inequalities and related systems (eds. Kuhn, H. W. and Tucker, A. W.), Annals of Mathematics Studies 38 (Princeton University Press, Princeton, 1956) pp. 19–40.Google Scholar
[11]Howie, J. M., Fundamentals of semigroup theory (Clarendon Press, Oxford, 1995).CrossRefGoogle Scholar
[12]Jones, P. R., ‘Analogues of the bicyclic semigroup in simple semigroups without idempotents’, Proc. Roy. Soc. Edinburgh Sect. A 106 A (1987), 11–24.CrossRefGoogle Scholar
[13]Mashevitzky, G. I., ‘On the finite basis problem for left hereditary systems of semigroup identities’,in: Semigroups, automata and languages (eds. Almeida, J., Gomes, G. M. and Silva, P. V.) (World Scientific, Singapore, 1996) pp. 167–181.Google Scholar
[14]McKenzie, R. N., McNulty, G. F. and Taylor, W. F., Algebras, lattices, varieties, Vol. I (Wadsworth & Brooks/Cole, Monterey, 1987).Google Scholar
[15]Megyesi, L. and Pollàk, G., ‘On simple principal ideal semigroups’, Studia Sci. Math. Hungar. 16 (1981), 437–448.Google Scholar
[16]Minkowski, H., Geometrie der Zahlen (Teubner, Leipzig, 1910).Google Scholar
[17]Motzkin, T., Beiträge zur Theorie der linearen Ungleichungen (Azriel, Jerusalem, 1936).Google Scholar
[18]Munn, W. D. and Reilly, N. R., ‘Congruences on a bisimple ω-semigroup’, Proc. Glasgow Math. Assoc. 7 (1966), 184–192.CrossRefGoogle Scholar
[19]Pastijn, F., ‘Semigroup varieties in which some Green relations coincide’, submitted.Google Scholar
[20]Pastijn, F. and Yan, X., ‘Completely regular semigroups in the variety generated by the bicyclic semigroup’, Algebra Universalis 30 (1993), 234–240.CrossRefGoogle Scholar
[21]Rankin, S. A. and Reis, C. M., ‘Semigroups with quasi-zeroes’, Canad. J. Math. 32 (1980), 511–530.CrossRefGoogle Scholar
[22]Rédei, L., ‘Halbgruppen und Ringe mit Linkseinheiten ohne Linkseinselemente’, Acta Math. Acad. Sci. Hungar. 11 (1960), 217–222.CrossRefGoogle Scholar
[23]Schleifer, F. G., ‘Looking for identities on a bicyclic semigroup with computer assistance’, Semigroup Forum 41 (1990), 173–179.CrossRefGoogle Scholar
[24]Schneerson, L. M., ‘On the axiomatic rank of varieties generated by a semigroup or monoid with one defining relation’, Semigroup Forum 39 (1989), 17–38.CrossRefGoogle Scholar
[25]Trotter, P. G., ‘Cancellative simple semigroups and groups’, Semigroup Forum 14 (1977), 189–198.CrossRefGoogle Scholar