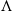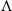Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ahmed, Suman
Aribam, Chandrakant
and
Shekhar, Sudhanshu
2017.
Root numbers and parity of local Iwasawa invariants.
Journal of Number Theory,
Vol. 177,
Issue. ,
p.
285.
Hatley, Jeffrey
2017.
Rank parity for congruent supersingular elliptic curves.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 9,
p.
3775.
KITAJIMA, Takahiro
and
OTSUKI, Rei
2018.
On the Plus and the Minus Selmer Groups for Elliptic Curves at Supersingular Primes.
Tokyo Journal of Mathematics,
Vol. 41,
Issue. 1,
Ponsinet, Gautier
2020.
On the structure of signed Selmer groups.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1635.
Sujatha, Ramdorai
2020.
Selmer groups in Iwasawa theory and congruences.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 378,
Issue. 2163,
p.
20180442.
LEI, Antonio
and
SUJATHA, Ramdorai
2020.
On Selmer Groups in the Supersingular Reduction Case.
Tokyo Journal of Mathematics,
Vol. 43,
Issue. 2,
AHMED, SUMAN
and
LIM, MENG FAI
2020.
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 101,
Issue. 2,
p.
238.
Ahmed, Suman
and
Lim, Meng Fai
2021.
On the Algebraic Functional Equation of the Eigenspaces of Mixed Signed Selmer Groups of Elliptic Curves with Good Reduction at Primes above p.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 2,
p.
289.
Kim, Chan-Ho
and
Kurihara, Masato
2021.
On the Refined Conjectures on Fitting Ideals of Selmer Groups of Elliptic Curves with Supersingular Reduction.
International Mathematics Research Notices,
Vol. 2021,
Issue. 14,
p.
10559.
Kim, Byoung Du
2021.
Congruences of algebraic p-adic L-functions and the Main Conjecture of Iwasawa Theory.
Journal of Number Theory,
Vol. 226,
Issue. ,
p.
168.
LIM, MENG FAI
2022.
On the cohomology of Kobayashi’s plus/minus norm groups and applications.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 1,
p.
1.
Kundu, Debanjana
and
Ray, Anwesh
2022.
Iwasawa invariants for elliptic curves over ℤ
p
-extensions and Kida's formula.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Hamidi, Parham
and
Ray, Jishnu
2022.
Conjecture A andμ-invariant for Selmer groups of supersingular elliptic curves.
Journal de Théorie des Nombres de Bordeaux,
Vol. 33,
Issue. 3.1,
p.
853.
Lei, Antonio
and
Lim, Meng Fai
2022.
Akashi series and Euler characteristics of signed Selmer groups of elliptic curves with semistable reduction at primes above p.
Journal de Théorie des Nombres de Bordeaux,
Vol. 33,
Issue. 3.2,
p.
997.
Hatley, Jeffrey
and
Lei, Antonio
2023.
The vanishing of anticyclotomic μ-invariants for non-ordinary modular forms.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G1,
p.
65.
Ray, Anwesh
and
Sujatha, R.
2023.
Euler characteristics and their congruences for multisigned Selmer groups.
Canadian Journal of Mathematics,
Vol. 75,
Issue. 1,
p.
298.
Hatley, Jeffrey
and
Kundu, Debanjana
2023.
$$\lambda $$-Invariant stability in families of modular Galois representations.
Research in the Mathematical Sciences,
Vol. 10,
Issue. 3,
Kim, Byoung Du BD
2024.
Iwasawa theory of plus/minus Selmer groups with non-co-free plus/minus local conditions.
International Journal of Number Theory,
Vol. 20,
Issue. 03,
p.
747.
Kim, Chan-Ho
and
Sujatha, R.
2024.
Class Groups of Number Fields and Related Topics.
Vol. 470,
Issue. ,
p.
25.
Shii, Ryota
2025.
On $$\Lambda $$-submodules with finite index of the plus/minus Selmer group over anticyclotomic $${{\,\mathrm{\mathbb {Z}}\,}}_{p}$$-extension at inert primes.
Annales mathématiques du Québec,