Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Xia
2003.
Quadratic functionals and small ball probabilities for the $m$-fold integrated Brownian motion.
The Annals of Probability,
Vol. 31,
Issue. 2,
Zhang, Rongmao
and
Lin, Zhengyan
2006.
A Functional LIL for m-Fold Integrated Brownian Motion*.
Chinese Annals of Mathematics, Series B,
Vol. 27,
Issue. 4,
p.
459.
Zhang, Rongmao
and
Lin, Zhengyan
2007.
Chung LIL for integrated stable process.
Statistics & Probability Letters,
Vol. 77,
Issue. 3,
p.
295.
Zhang, Rong Mao
and
Lin, Zheng Yan
2010.
A functional LIL for integrated α stable process.
Acta Mathematica Sinica, English Series,
Vol. 26,
Issue. 2,
p.
393.
Lachal, Aimé
2011.
A Class of Bridges of Iterated Integrals of Brownian Motion Related to Various Boundary Value Problems Involving the One-Dimensional Polyharmonic Operator.
International Journal of Stochastic Analysis,
Vol. 2011,
Issue. ,
p.
1.


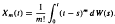 Watanabe and Lachal gave some asymptotic properties of the process
Watanabe and Lachal gave some asymptotic properties of the process 