Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-08T21:37:39.318Z Has data issue: false hasContentIssue false
  • English
  • Français

PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS

Part of: Discontinuous groups and automorphic forms Curves Arithmetic algebraic geometry

Published online by Cambridge University Press:  19 August 2015

FRANÇOIS BRUNAULT
FRANÇOIS BRUNAULT*
Affiliation:
ÉNS Lyon, UMPA, 46 allée d’Italie, 69007 Lyon, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that every elliptic curve over the rationals admits a parametrization by means of modular functions. In this short note, we show that only finitely many elliptic curves over 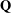$\mathbf{Q}$ can be parametrized by modular units. This answers a question raised by W. Zudilin in a recent work on Mahler measures. Further, we give the list of all elliptic curves 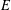$E$ of conductor up to 1000 parametrized by modular units supported in the rational torsion subgroup of 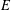$E$. Finally, we raise several open questions.

Keywords

elliptic curvesmodular parametrizationmodular units

MSC classification

Primary: 11F03: Modular and automorphic functions
Secondary: 11G05: Elliptic curves over global fields 11G16: Elliptic and modular units 14H52: Elliptic curves
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 1 , February 2016 , pp. 33 - 41
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Baker, M. H., González-Jiménez, E., González, J. and Poonen, B., ‘Finiteness results for modular curves of genus at least 2’, Amer. J. Math. 6(127) (2005), 1325–1387.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Boyd, D. W., ‘Mahler’s measure and special values of L-functions’, Experiment. Math. 1(7) (1998), 37–82.CrossRefGoogle Scholar
Brunault, F., ‘On the ramification of modular parametrizations at the cusps’, Preprint, 2012http://arxiv.org/abs/1206.2621.Google Scholar
Cremona, J. E., Algorithms for Modular Elliptic Curves, 2nd edn (Cambridge University Press, Cambridge, 1997).Google Scholar
Deninger, C., ‘Deligne periods of mixed motives, K-theory and the entropy of certain Zn-actions’, J. Amer. Math. Soc. 2(10) (1997), 259–281.CrossRefGoogle Scholar
Ribet, K. A., ‘Abelian varieties over Q and modular forms’, in: Modular Curves and Abelian Varieties, Progress in Mathematics, 224 (Birkhäuser, Basel, 2004), 241–261.CrossRefGoogle Scholar
Shimura, G., Introduction to the Arithmetic Theory of Automorphic Functions, Kano Memorial Lectures, 1; Publications of the Mathematical Society of Japan, 11 (Princeton University Press, Princeton, NJ, 1994).Google Scholar
Stevens, G., ‘Stickelberger elements and modular parametrizations of elliptic curves’, Invent. Math. 1(98) (1989), 75–106.CrossRefGoogle Scholar
The PARI Group, Bordeaux, PARI/GP version 2.7.3, available from http://pari.math.u-bordeaux.fr/.Google Scholar
Watkins, M., ‘Explicit lower bounds on the modular degree of an elliptic curve’, Preprint, 2004http://arxiv.org/abs/math/0408126.Google Scholar
Zudilin, W., ‘Regulator of modular units and Mahler measures’, Math. Proc. Cambridge Philos. Soc. 2(156) (2014), 313–326.CrossRefGoogle Scholar