Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T14:07:34.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Pairs of additive congruences to a large prime modulus

Part of: Diophantine equations

Published online by Cambridge University Press:  09 April 2009

O. D. Atkinson  and
R. J. Cook
O. D. Atkinson
Affiliation:
Department of Pure Mathematics, University of Sheffield, Sheffield S3 7RH, England
R. J. Cook
Affiliation:
Department of Pure Mathematics, University of Sheffield, Sheffield S3 7RH, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with non-trivial solvability in p–adic integers, for relatively large primes p, of a pair of additive equations of degree k > 1: 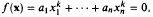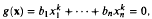where the coefficients a1,…, an, b1,…, bn are rational integers.

Our first theorem shows that the above equations have a non-trivial solution in p–adic integers if n > 4k and p > k6. The condition on n is best possible.

The later part of the paper obtains further information for the particular case k = 5. specifically we show that when k = 5 the above equations have a non-trivial solution in p–adic integers (a) for all p > 3061 if n ≥ 21; (b) for all p execpt p = 5, 11 if n ≥ 26.

MSC classification

Secondary: 11D88: $p$-adic and power series fields
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 46 , Issue 3 , June 1989 , pp. 438 - 455
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Atkinson, O. D. (PhD Dissertation, University of Sheffield, 1989).Google Scholar
[2]Baker, R. C. and Brüden, J., ‘On pairs of additive cubic equations’, J. Reine Angew. Math. 391 (1988), 157–180.Google Scholar
[3]Borevich, Z. I. and Shafarevich, I. R., Number theory (Academic Press, New York, 1966).Google Scholar
[4]Chowla, I., ‘On the number of solutions of some congruences in two variables’, Proc. Nat. Acad. Sci. India Ser. A 5 (1937), 40–44.CrossRefGoogle Scholar
[5]Chowla, S., Mann, H. B. and Straus, E. G., ‘Some applications of the Cauchy-Davenport theorem’, Norske Vid. Selsk. Forh. 32 (1959), 74–80.Google Scholar
[6]Cook, R. J., ‘Pairs of additive equations’, Michigan Math. J. 19 (1972), 325–331.CrossRefGoogle Scholar
[7]Cook, R. J., ‘Pairs of additive congruences: cubic congruences’, Mathematika 32 (1985), 286–300.CrossRefGoogle Scholar
[8]Cook, R. J., ‘Pairs of additive congruences: quintic congruences’, Indian J. Pure Appl. Math. 17 (1986), 786–799.Google Scholar
[9]Cook, R. J., ‘Computations for additive Diophantine equations: quintic congruences II’, Computers in Mathematical Research, edited by Stephens, N. M. and Thorne, M. P., pp. 93–117 (Clarendon Press, Oxford, 1988).Google Scholar
[10]Davenport, H., Analytic methods for Diophantine equations and diophantine inequalities (Campus Publishers, Ann Arbor, 1963).Google Scholar
[11]Davenport, H. and Lewis, D. J., ‘Homogeneous additive equations’, Proc. Roy. Soc. London Ser A 274 (1963), 443–460.Google Scholar
[12]Davenport, H. and Lewis, D. J., ‘Cubic equations of additive type’, Philos. Trans. Roy. Soc. London Ser. A 261 (1966), 97–136.Google Scholar
[13]Davenport, H. and Lewis, D. J., ‘Notes on congruences III’, Quart. J. Math. Oxford Ser (2), 17 (1966), 339–344.CrossRefGoogle Scholar
[14]Davenport, H. and Lewis, D. J., ‘Two additive equations’, Proc. Sympos. Pure Math. 12 (1967), 74–98.CrossRefGoogle Scholar
[15]Davenport, H. and Lewis, D. J., ‘Simultaneous equations of additive type’, Philos. Trans. Roy. Soc. London Ser. A 264 (1969), 557–595.Google Scholar
[16]Demyanov, V. B., ‘Pairs of quardratic forms over a complete field with discrete norm with finite residue class field’, Izv. Akad. Nauk SSSR 20 (1956), 307–324.Google Scholar
[17]Dodson, M. M., ‘Homogeneous additive congruences’, Philos. Trans. Roy. Soc. London Ser A 261 (1966), 163–210.Google Scholar
[18]Ellison, F., ‘Three diagonal quadratic forms’, Acta Arith. 23 (1973), 137–151.CrossRefGoogle Scholar
[19]Gray, J. F., Diagonal forms of prime degree (PhD thesis, University of Notre Dame, 1958).Google Scholar
[20]Lewis, D. J., ‘Cubic congruences’, Michigan Math. J. 4 (1957), 85–95.CrossRefGoogle Scholar
[21]Low, L., Pitman, J. and Wolff, A., ‘Simultaneous diagonal congruences’, J. Number Theory 29 (1988), 31–59.CrossRefGoogle Scholar
[22]Schmidt, W. M., ‘The solubility of certain p–adic equations’, J. Number Theory 19 (1984), 63–80.CrossRefGoogle Scholar
[23]Stevenson, E., ‘The Artin conjecture for three diagonal cubic forms’, J. Number Theory 14 (1982), 374–390.CrossRefGoogle Scholar
[24]Vaughan, R. C., ‘On pairs of additive cubic equations’, Proc. London Math. Soc. 34 (1977), 354–364.CrossRefGoogle Scholar
[25]Vaughan, R. C., ‘On Waring's problem for smaller exponents’, Proc. London Math. Soc. 52 (1986), 445–463.CrossRefGoogle Scholar