Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T13:37:04.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthomorphisms of a commutative W*-algebra

Part of: Topological linear spaces and related structures

Published online by Cambridge University Press:  09 April 2009

P. G. Dodds
P. G. Dodds
Affiliation:
The Flinders University of South AustraliaBedford Park, S.A. 5042, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If M is a commutative W*-algebra of operators and if ReM is the Dedekind complete Riesz space of self-adjoint elements of M, then it is shown that the set 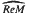of densely defined self-adjoint transformations affiliated with ReM is a Dedekind complete, laterally complete Riesz algebra containing ReM as an order dense ideal. The Riesz algebra of densely defined orthomorphisms on ReM is shown to coincide with 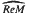, and via the vector lattice Randon-Nikodym theorem of Luxemburg and Schep, it is shown that the lateral completion of ReM may be identified with the extended order dual of ReM.

MSC classification

Secondary: 46A40: Ordered topological linear spaces, vector lattices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 37 , Issue 2 , October 1984 , pp. 143 - 168
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Bernau, S. J., ‘The square root of a positive self-adjoint operator’, J. Austral. Math. Soc. 8 (1967), 17–36.CrossRefGoogle Scholar
[2]Dixmier, J., Les algèbres d'opérateurs dans l'espace Hilbertien (Gauthier-Villars, Paris, 1957).Google Scholar
[3]Dixmier, J., ‘Sur certains espaces considérés par M. H. Stone’, Summa Brasil. Math. 2 (1951), 151–182.Google Scholar
[4]Dodds, P. G., “The order dual of an abelian von Neumann algebra’, J. Austral. Math. Soc. 28 (1974), 153–160.CrossRefGoogle Scholar
[5]Duhoux, M. and Meyer, M., ‘A new proof of the lattice structure of orthomorphisms’, J. London Math. Soc. (2) 25 (1982), 375–378.CrossRefGoogle Scholar
[6]Duhoux, M. and Meyer, M., Extended orthomorphisms on Archimedean Riesz spaces, Rapport n°114 (1981), Séminaire de Mathématique Pure et Appliquée, Université Catholique de Louvain.Google Scholar
[7]Dunford, N. and Schwartz, J. T., Linear operators, Part II, Interscience, New York, 1963.Google Scholar
[8]Luxemburg, W. A. J., Some aspects of the theory of Riesz spaces (Lecture Notes in Mathematics 4, University of Arkansas, Fayetteville, 1979).Google Scholar
[9]Luxemburg, W. A. J. and Masterson, J. J., ‘An extension of the concept of the order dual of a Riesz space’, Canad. J. Math. 19 (1967), 488–498.CrossRefGoogle Scholar
[10]Luxemburg, W. A. J. and Schep, A. R., ‘A Radon-Nikodym theorem for positive operators and a dual’, Nederl. Adad. Wetensch. Proc. Ser. A 81 (3) (1978), 357–375.Google Scholar
[11]Luxemburg, W. A. J. and Zaanen, A. C., Riesz spaces I (North-Holland Mathematical Library, Amsterdam, 1972).Google Scholar
[12]Murray, F. and von Neumann, J., ‘On rings of operators’, Ann. of Math. 37 (1936), 116–229.CrossRefGoogle Scholar
[13]Sz-Nagy, B. v., Spektraldarsartellung linearer Transformationen des Hilbertschen Raumes (Ergebnisse Math. Band 5, Springer, Berlin, 1942).CrossRefGoogle Scholar
[14]Nakamura, M. and Takeda, Z., ‘The Radon-Nikodym theorem of traces for a certain operator algebra’, Tôhoku Math. J. 4 (1952), 275–283.CrossRefGoogle Scholar
[15]Nakano, H., ‘Teilweise geordnete Algebra’, Japan J. Math. 17 (1941), 425–511.CrossRefGoogle Scholar
[16]de Pagter, B., f-algebras and orthomorphisms (Thesis, University of Leiden, 1981).Google Scholar
[17]Riesz, F. and Sz-Nagy, B. v., Functional analysis (Ungar, New York, 1955).Google Scholar
[18]Vulikh, B. Z., Introduction to the theory of partially ordered spaces (Wolters-Noordhoff, Groningen, 1967).Google Scholar
[19]Wouk, A., ‘A note on square roots of positive operators’, SIAM Rev. (1966), 100–102.CrossRefGoogle Scholar
[20]Wickstead, A. W., ‘Representation and duality of multiplication operators on Riesz spaces’, Compositio. Math. 35 (1977), 225–238.Google Scholar
[21]Wickstead, A. W., ‘Extensions of orthomorphisms’, J. Austral. Math. Soc. Ser. A 29 (1980), 87–98.CrossRefGoogle Scholar
[22]Zaanen, A. C., ‘Examples of orthomorphisms’, J. Approximation Theory 13 (1975), 192–204.Google Scholar