Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-20T06:43:48.309Z Has data issue: false hasContentIssue false
  • English
  • Français

ORIGAMI RINGS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  02 November 2012

JOE BUHLER ,
STEVE BUTLER ,
WARWICK DE LAUNEY  and
RON GRAHAM
JOE BUHLER
Affiliation:
Center for Communications Research, La Jolla, CA 92121, USA (email: [email protected])
STEVE BUTLER*
Affiliation:
Department of Mathematics, Iowa State University, Ames, IA, 50011, USA (email: [email protected])
WARWICK DE LAUNEY
Affiliation:
Center for Communications Research, La Jolla, CA 92121, USA
RON GRAHAM
Affiliation:
Department of Computer Science and Engineering, University of California, San Diego, La Jolla, CA 92093, USA (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by mathematical aspects of origami, Erik Demaine asked which points in the plane can be constructed by using lines whose angles are multiples of 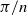$\pi /n$ for some fixed $n$. This has been answered for some specific small values of $n$ including 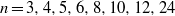$n=3,4,5,6,8,10,12,24$. We answer this question for arbitrary $n$. The set of points is a subring of the complex plane 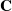$\mathbf {C}$, lying inside the cyclotomic field of $n$th roots of unity; the precise description of the ring depends on whether $n$is prime or composite. The techniques apply in more general situations, for example, infinite sets of angles, or more general constructions of subsets of the plane.

Keywords

origamiringscyclotomic fieldsbinary hybridization

MSC classification

Secondary: 11R04: Algebraic numbers; rings of algebraic integers
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 92 , Issue 3 , June 2012 , pp. 299 - 311
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc.

References

[1]Alperin, R. C., ‘A mathematical theory of origami constructions and numbers’, New York J. Math. 6 (2000), 119–133.Google Scholar
[2]Alperin, R. C. and Lang, R. J., ‘One-, two-, and multi-fold origami axioms’, in: Origami4 (A K Peters, Natick, MA, 2009), pp. 371–393.Google Scholar
[3]Demaine, E. D. and O’Rourke, J., Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Cambridge University Press, Cambridge, 2007).CrossRefGoogle Scholar
[4]Origami5: Fifth International Meeting of Origami Science, Mathematics, and Education (A K Peters/CRC Press, Natick, MA, 2011).Google Scholar
[5]Lang, R. J., Origami Design Secrets (A K Peters, Natick, MA, 2003).CrossRefGoogle Scholar
[6]Lang, R. J., ReferenceFinder, available online at http://www.langorigami.com/science/reffinder/reffinder.php4.Google Scholar
[7]Tachi, T. and Demaine, E., ‘Degenerative coordinates in $22.5^\circ $ grid system’, in: Origami5: Fifth International Meeting of Origami Science, Mathematics, and Education (A K Peters/CRC Press, Natick, MA, 2011).Google Scholar
[8]Washington, L., Introduction to Cyclotomic Fields, 2nd edn (Springer, New York, 1997).CrossRefGoogle Scholar