Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-02T17:25:55.522Z Has data issue: false hasContentIssue false
  • English
  • Français

ON WARING’S PROBLEM IN SUMS OF THREE CUBES FOR SMALLER POWERS

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  16 September 2021

JAVIER PLIEGO
JAVIER PLIEGO*
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067, USA e-mail: [email protected] and School of Mathematics, University of Bristol, Fry Building, Woodland Road, Bristol, BS8 1UG, UK
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an upper bound for the minimum s with the property that every sufficiently large integer can be represented as the sum of s positive kth powers of integers, each of which is represented as the sum of three positive cubes for the cases 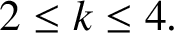$2\leq k\leq 4.$

Keywords

Waring’s problemHardy–Littlewood method

MSC classification

Primary: 11P05: Waring's problem and variants
Secondary: 11P55: Applications of the Hardy-Littlewood method
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 114 , Issue 3 , June 2023 , pp. 378 - 405
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by D. Badziahin

The author’s work was supported in part by a European Research Council Advanced Grant under the European Union’s Horizon 2020 research and innovation programme via grant agreement no. 695223 during his studies at the University of Bristol.

References

Bourgain, J., ‘On $\varLambda (p)-$ subsets of squares’, Israel J. Math. 67(3) (1989), 291–311.CrossRefGoogle Scholar
Davenport, H., ‘On Waring’s problem for fourth powers’, Ann. of Math. (2) 40 (1939), 731–747.CrossRefGoogle Scholar
Davenport, H., Analytic Methods for Diophantine Equations and Diophantine Inequalities, 2nd edn (ed. Browning, T. D.) Cambridge Mathematical Library (Cambridge University Press, Cambridge, 2005).CrossRefGoogle Scholar
Heath-Brown, D. R., ‘The circle method and diagonal cubic forms’, Philos. Trans. Roy. Soc. A 356(1738) (1998), 673–699.CrossRefGoogle Scholar
Hooley, C., ‘On Waring’s problem’, Acta Math. 157 (1986), 49–97.CrossRefGoogle Scholar
Hooley, C., ‘On hypothesis K* in Waring’s problem’, in: Sieve Methods, Exponential Sums and Their Applications in Number Theory (Cardiff, 1995), (eds. Greaves, G. R. H., Harman, G. and Huxley, M. N.) London Mathematical Society Lecture Note Series, 237 (Cambridge University Press, Cambridge, 1997), 175–185.CrossRefGoogle Scholar
Hughes, K. and Wooley, T. D., ‘Discrete restriction for $(x,{x}^3)$ and related topics’, Preprint, 2019.Google Scholar
Linnik, Y. V., ‘On the representation of large numbers as sums of seven cubes’, Rec. Math. (N.S.) 12(54) (1943), 218–224.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory: I. Classical Theory (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Pliego, J., ‘On squares of sums of three cubes’, Q. J. Math. 71(4) (2020), 1219–1235.CrossRefGoogle Scholar
Pliego, J., ‘On Waring’s problem in sums of three cubes’, Mathematika 67(1) (2021), 235–256.CrossRefGoogle Scholar
Pliego, J., ‘Uniform bounds in Waring’s problem over some diagonal forms’, Preprint, 2020.CrossRefGoogle Scholar
Schmidt, W. M., Equations over Finite Fields. An Elementary Approach, Lecture Notes in Mathematics, 536 (Springer, Berlin, 1976).CrossRefGoogle Scholar
Vaughan, R. C., ‘On Waring’s problem for smaller exponents’, Proc. Lond. Math. Soc. (3) 52 (1986), 445–463.CrossRefGoogle Scholar
Vaughan, R. C., ‘A new iterative method in Waring’s problem’, Acta Math. 162 (1989), 1–71.CrossRefGoogle Scholar
Vaughan, R. C., The Hardy–Littlewood Method, 2nd edn (Cambridge University Press, Cambridge, 1997).CrossRefGoogle Scholar
Vaughan, R. C. and Wooley, T. D., Further improvements in Waring’s problem. II. Sixth powers’, Duke Math. J. 76(3) (1994), 683–710.CrossRefGoogle Scholar
Vaughan, R. C. and Wooley, T. D., ‘Further improvements in Waring’s problem. IV. Higher powers’, Acta Arith. 94(3) (2000), 203–285.CrossRefGoogle Scholar
Weil, A., ‘On some exponential sums’, Proc. Natl. Acad. Sci. USA 34 (1948), 204–207.CrossRefGoogle ScholarPubMed
Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis (Cambridge University Press, Cambridge, 1927).Google Scholar
Wooley, T. D., ‘New estimates for smooth Weyl sums’, J. Lond. Math. Soc. (2) 51(1) (1995), 1–13.CrossRefGoogle Scholar
Wooley, T. D., ‘Sums of three cubes, II’, Acta Arith. 170(1) (2015), 73–100.CrossRefGoogle Scholar
Wooley, T. D., ‘On Waring’s problem for intermediate powers’, Acta Arith. 176(3) (2016), 241–247.CrossRefGoogle Scholar
Wooley, T. D., ‘Nested efficient congruencing and relatives of Vinogradov’s mean value theorem’, Proc. Lond. Math. Soc. (3) 118(4) (2019), 942–1016.CrossRefGoogle Scholar