Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T07:22:25.091Z Has data issue: false hasContentIssue false
  • English
  • Français

On unilateral shift operators and C0-operators

Part of: Commutative Banach algebras and commutative topological algebras Special classes of linear operators

Published online by Cambridge University Press:  09 April 2009

Il Bong Jung  and
Yong Chan Kim
Il Bong Jung
Affiliation:
College of Natural SciencesKyungpook National UniversityTaegu, 702-701, Korea
Yong Chan Kim
Affiliation:
College of EducationYeungnam UniversityGyongsan, 713–749, Korea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S(n) be a unilateral shift operator on a Hilbert space of multiplicity n. In this paper, we prove a generalization of the theorem that if S(1) is unitarily equivalent to an operator matrix form 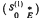relative to a decomposition ℳ ⊕ N, then E is in a certain class C0 which will be defined below.

MSC classification

Secondary: 47B37: Operators on special spaces (weighted shifts, operators on sequence spaces, etc.) 46J15: Banach algebras of differentiable or analytic functions, $H^p$-spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 53 , Issue 1 , August 1992 , pp. 137 - 142
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Bercovici, H., Operator theory and arithmetic in H∞ Math. Surveys and Monographs, No. 26, (Amer. Math. Soc., Providence, R.I., 1988).CrossRefGoogle Scholar
[2]Brown, A. and Pearcy, C., Introduction to operator theory. I, Elements of functional analysis (Springer-Verlag, New York, 1977).Google Scholar
[3]Conway, J., Subnormal operators (Pitman, Boston, 1981).Google Scholar
[4]Hoffman, K., Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N.J., 1962).Google Scholar
[5]Jung, I., Dual operator algebras and the classes Am, n (Ph.D. Thesis, Univ. of Michigan, 1989).Google Scholar
[6]-Nagy, B. Sz. and Foiaş, C., Harmonic analysis of operators on the Hilbert space (North Holland Akademiai Kiado, Amsterdam/Budapest, 1970).Google Scholar