Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T09:15:57.306Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE UMBILICITY OF HYPERSURFACES IN THE HYPERBOLIC SPACE

Part of: Global differential geometry Local differential geometry General relativity Applications to physics - Differential geometry

Published online by Cambridge University Press:  16 November 2016

C. P. AQUINO ,
M. BATISTA  and
H. F. DE LIMA
C. P. AQUINO
Affiliation:
Departamento de Matemática, Universidade Federal do Piauí, 64049-550 Teresina, Piauí, Brazil email [email protected]
M. BATISTA*
Affiliation:
Instituto de Matemática, Universidade Federal de Alagoas, 57072-970 Maceió, Alagoas, Brazil email [email protected]
H. F. DE LIMA
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58429-970 Campina Grande, Paraíba, Brazil email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we establish new characterization results concerning totally umbilical hypersurfaces of the hyperbolic space 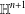$\mathbb{H}^{n+1}$, under suitable constraints on the behavior of the Lorentzian Gauss map of complete hypersurfaces having some constant higher order mean curvature. Furthermore, working with different warped product models for 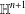$\mathbb{H}^{n+1}$ and supposing that certain natural inequalities involving two consecutive higher order mean curvature functions are satisfied, we study the rigidity and the nonexistence of complete hypersurfaces immersed in 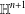$\mathbb{H}^{n+1}$.

Keywords

hyperbolic spacecomplete hypersurfacestotally umbilical hypersurfaceshigher order mean curvaturesLorentzian Gauss map

MSC classification

Primary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Secondary: 53B30: Lorentz metrics, indefinite metrics 53C50: Lorentz manifolds, manifolds with indefinite metrics 53Z05: Applications to physics 83C99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 45 - 58
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is partially supported by CNPq, Brazil, grant number 302738/2014-2. The second author is partially supported by CNPq, Brazil, grant number 456755/2014-4. The third author is partially supported by CNPq, Brazil, grant number 303977/2015-9.

References

Aledo, J., Alías, L. J. and Romero, A., ‘Integral formulas for compact space-like hypersurfaces in de Sitter space: applications to the case of constant higher order mean curvature’, J. Geom. Phys. 31 (1999), 195–208.Google Scholar
Alías, L. J. and Dajczer, M., ‘Uniqueness of constant mean curvature surfaces properly immersed in a slab’, Comment. Math. Helv. 81 (2006), 653–663.Google Scholar
Alías, L. J., Kurose, T. and Solanes, G., ‘Hadamard-type theorems for hypersurfaces in hyperbolic spaces’, Differential Geom. Appl. 24 (2006), 492–502.Google Scholar
Aquino, C. P., ‘On the Gauss mapping of hypersurfaces with constant scalar curvature in ℍ n+1 ’, Bull. Braz. Math. Soc. 45 (2014), 117–131.Google Scholar
Aquino, C. P., Barros, A. and de Lima, H. F., ‘Complete CMC hypersurfaces in the hyperbolic space with prescribed Gauss mapping’, Proc. Amer. Math. Soc. 142 (2014), 3597–3604.Google Scholar
Aquino, C. P. and de Lima, H. F., ‘On the Gauss map of complete CMC hypersurfaces in the hyperbolic space’, J. Math. Anal. Appl. 386 (2012), 862–869.Google Scholar
Aquino, C. P. and de Lima, H. F., ‘On the geometry of horospheres’, Comment. Math. Helv. 89 (2014), 617–629.Google Scholar
Barbosa, J. L. and Colares, A. G., ‘Stability of hypersurfaces with constant r-mean curvature’, Ann. Global Anal. Geom. 15 (1997), 277–297.Google Scholar
Camargo, F., Caminha, A. and de Lima, H. F., ‘Bernstein-type theorems in semi-Riemannian warped products’, Proc. Amer. Math. Soc. 139 (2011), 1841–1850.Google Scholar
Caminha, A., ‘The geometry of closed conformal vector fields on Riemannian spaces’, Bull. Braz. Math. Soc. 42 (2011), 277–300.CrossRefGoogle Scholar
Caminha, A. and de Lima, H. F., ‘Complete vertical graphs with constant mean curvature in semi-Riemannian warped products’, Bull. Belg. Math. Soc. 16 (2009), 91–105.Google Scholar
do Carmo, M. and Lawson, B., ‘The Alexandrov–Bernstein theorems in hyperbolic space’, Duke Math. J. 50 (1983), 995–1003.Google Scholar
Karp, L., ‘On Stokes’ theorem for noncompact manifolds’, Proc. Amer. Math. Soc. 82 (1981), 487–490.Google Scholar
López, R. and Montiel, S., ‘Existence of constant mean curvature graphs in hyperbolic space’, Calc. Var. 8 (1999), 177–190.Google Scholar
Montiel, S., ‘An integral inequality for compact spacelike hypersurfaces in de Sitter space and applications to the case of constant mean curvature’, Indiana Univ. Math. J. 37 (1988), 909–917.Google Scholar
Montiel, S., ‘Unicity of constant mean curvature hypersurfaces in some Riemannian manifolds’, Indiana Univ. Math. J. 48 (1999), 711–748.Google Scholar
Montiel, S. and Ros, A., ‘Compact hypersurfaces: the Alexandrov theorem for higher order mean curvatures’, in: Differential Geometry, Pitman Monographs and Surveys in Pure and Applied Mathematics, 52 (eds. Lawson, B. and Tenenblat, K.) (Longman Scientific & Technical, Harlow, 1991), 279–296.Google Scholar
Reilly, R., ‘Variational properties of functions of the mean curvature for hypersurfaces in space form’, J. Differential Geom. 8 (1973), 447–453.CrossRefGoogle Scholar
Rosenberg, H., ‘Hypersurfaces of constant curvature in space forms’, Bull. Sci. Math. 117 (1993), 217–239.Google Scholar
Shu, S., ‘Complete hypersurfaces with constant scalar curvature in a hyperbolic space’, Balkan J. Geom. Appl. 12 (2007), 107–115.Google Scholar
Wang, Q. and Xia, C., ‘Topological and metric rigidity theorems for hypersurfaces in a hyperbolic space’, Czechoslovak Math. J. 57 (2007), 435–445.Google Scholar
Yau, S. T., ‘Some function-theoretic properties of complete Riemannian manifolds and their applications to geometry’, Indiana Univ. Math. J. 25 (1976), 659–670.Google Scholar