Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-30T20:42:49.794Z Has data issue: false hasContentIssue false
  • English
  • Français

On the stability of linear canonical systems with periodic coefficients

Published online by Cambridge University Press:  09 April 2009

W. A. Coppel  and
A. Howe
W. A. Coppel
Affiliation:
The Australian National University, Canberra.
A. Howe
Affiliation:
The Australian National University, Canberra.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

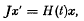By a linear canonical system we mean a system of linear differential equations of the form where J is an invertible skew-Hermitian matrix and H(t) is a continuous Hermitian matrix valued function. We reserve the name Hami1tonia for real canonical systems with 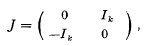where Ik denotes the k × k unit matrix. In recent years the stability properties of Hamiltonian systems whose coefficient matrix H(t) is periodic have been deeply investigated, mainly by Russian authors ([2], [3], [5], [7]). An excellent survey of the literature is given in [6]. The purpose of the present paper is to extend this theory to canonical systems. The only work which we know of in this direction is a paper by Yakubovič [9].

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 2 , May 1965 , pp. 169 - 195
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Chevalley, C., Theory of groups, I Princeton, 1946.Google Scholar
[2]Diliberto, S. P., On stability of linear mechanical systems, Proc. Internat. Sympos. Nonlinear Vibrations, Izdat. Akad. Nauk Ukrain. SSR, Kiev, 1963, Vol. 1, pp. 189–203.Google Scholar
[3]Gelfand, I. M. and Lidskji, V. B., On the structure of the domains of stability of linear canonical systems of differential equations with periodic coefficients (Russian), Uspehi Mat. Nauk (N.S.) 10 (1955) 3–40;Google Scholar
Amer. Math. Soc. Transl. (2) 8 (1958) 143–181.Google Scholar
[4]Jablonski, E., Théorie des permutations et des arrangements circulaires complets, J. Math. Pures Appl. (4) 8 (1892), 331–349.Google Scholar
[5]Kerin, M. G., The basic propositions in the theory of λ-zones of stability of a canonical system of linear differential equations with periodic coefficients (Russian), Pamyati A. A. Andronova, Izdat. Akad. Nauk. SSSR, Moscow, 1955, pp. 413–498.Google Scholar
[6]Krein, M. G. and Yakubovič, V. A., Hamiltonian system of linear differential equations with periodic coefficients (Russian), Proc. Internat. Sympos. Nonlinear Vibrations, Izdat. Akad. Nauk Ukrain. SSR, Kiev, 1963, Vol. 1, pp. 277–305.Google Scholar
[7]Moser, J., New aspects in the theory of stability of Hamiltonian systems, Comm. Pure Appl. Math. 11 (1958) 81–114.CrossRefGoogle Scholar
[8]Riesz, F. and Sz.-Nagy, B., Functional Analysis, New York, 1955, Chap. XI.Google Scholar
[9]Yakubovič, V. A., Critical frequencies of quasicanonical systems (Russian), Vestnik Leningrad Univ. 13 (1958) 35–63.Google Scholar
[10]Yakubovič, V. A., The small parameter method for canonical systems with periodic coefficients, J. Appl. Math. Mech. 23 (1959) 17–43.CrossRefGoogle Scholar