Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
44.
Filaseta, Michael
1996.
Analytic Number Theory.
p.
371.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
71.
Bennett, M. A.
Filaseta, M.
and
Trifonov, O.
2009.
On the factorization of consecutive integers.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2009,
Issue. 629,
Patassini, Massimiliano
2012.
Recognizing the Non-Frattini Abelian Chief Factors of a Finite Group from Its Probabilistic Zeta Function.
Communications in Algebra,
Vol. 40,
Issue. 12,
p.
4494.
Filaseta, Michael
Kidd, Travis
and
Trifonov, Ognian
2012.
Laguerre polynomials with Galois groupAmfor each m.
Journal of Number Theory,
Vol. 132,
Issue. 4,
p.
776.
Burness, Timothy C.
and
Hall, Emily V.
2022.
Almost elusive permutation groups.
Journal of Algebra,
Vol. 594,
Issue. ,
p.
519.


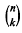 , where each prime factor of
, where each prime factor of 