Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T07:45:20.417Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE GROUP INVERSE FOR THE SUM OF MATRICES

Part of: Basic linear algebra

Published online by Cambridge University Press:  08 November 2013

CHANGJIANG BU ,
XIUQING ZHOU ,
LIANG MA  and
JIANG ZHOU
CHANGJIANG BU*
Affiliation:
College of Science, Harbin Engineering University, Harbin 150001, PR China
XIUQING ZHOU
Affiliation:
College of Science, Harbin Engineering University, Harbin 150001, PR China
LIANG MA
Affiliation:
College of Science, Harbin Engineering University, Harbin 150001, PR China
JIANG ZHOU
Affiliation:
College of Science, Harbin Engineering University, Harbin 150001, PR China
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 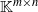${ \mathbb{K} }^{m\times n} $ denote the set of all 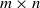$m\times n$ matrices over a skew field 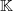$ \mathbb{K} $. In this paper, we give a necessary and sufficient condition for the existence of the group inverse of 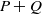$P+ Q$ and its representation under the condition 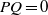$PQ= 0$, where 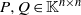$P, Q\in { \mathbb{K} }^{n\times n} $. In addition, in view of the natural characters of block matrices, we give the existence and representation for the group inverse of 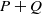$P+ Q$ and 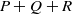$P+ Q+ R$ under some conditions, where 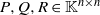$P, Q, R\in { \mathbb{K} }^{n\times n} $.

Keywords

group inversegroup invertibilityskew field

MSC classification

Secondary: 15A09: Matrix inversion, generalized inverses
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 1 , February 2014 , pp. 36 - 43
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Benítez, J., Liu, X. and Zhu, T., ‘Nonsingularity and group invertibility of linear combinations of two k-potent matrices’, Linear Multilinear Algebra 58 (2010), 1023–1035.Google Scholar
Benítez, J., Liu, X. and Zhu, T., ‘Additive results for the group inverse in an algebra with applications to block operators’, Linear Multilinear Algebra 59 (2011), 279–289.CrossRefGoogle Scholar
Bhaskara Rao, K. P. S., The Theory of Generalized Inverses over Commutative Rings (Taylor and Francis, London, 2002).Google Scholar
Bu, C., Feng, C. and Bai, S., ‘Representations for the Drazin inverses of the sum of two matrices and some block matrices’, Appl. Math. Comput. 218 (2012), 10 226–10 237.Google Scholar
Bu, C., Li, M., Zhang, K. and Zheng, L., ‘Group inverse for the block matrices with an invertible subblock’, Appl. Math. Comput. 215 (2009), 132–139.Google Scholar
Bu, C., Zhang, K. and Zhao, J., ‘Some results on the group inverse of the block matrix with a sub-block of linear combination or product combination of matrices over skew fields’, Linear Multilinear Algebra 58 (2010), 957–966.Google Scholar
Bu, C., Zhao, J. and Zheng, J., ‘Group inverse for a class $2\times 2$ block matrices over skew fields’, Appl. Math. Comput. 204 (2008), 45–49.Google Scholar
Campbell, S. L. and Meyer, C. D., Generalized Inverses of Linear Transformations (Dover, New York, 1991).Google Scholar
Cao, C., ‘Some results of group inverses for partitioned matrices over skew fields’, J. Natural Sci. Heilongjiang Univ. 18 (3) (2001), 5–7 (in Chinese).Google Scholar
Cao, C. and Li, J. M., ‘A note on the group inverse of some $2\times 2$ block matrices over skew fields’, Appl. Math. Comput. 217 (2011), 10 271–10 277.Google Scholar
Cao, C. and Li, J. Y., ‘Group inverses for matrices over a Bezout domain’, Electron. J. Linear Algebra 18 (2009), 600–612.Google Scholar
Cvetković-Ilić, D. S., ‘New additive results on Drazin inverse and its applications’, Appl. Math. Comput. 218 (2011), 3019–3024.Google Scholar
Cvetković-Ilić, D. S. and Deng, C. Y., ‘The Drazin invertibility of the difference and the sum of two idempotent operators’, J. Comput. Appl. Math. 233 (2010), 1717–1732.Google Scholar
Hartwig, R. E., Wang, G. and Wei, Y., ‘Some additive results on Drazin inverse’, Linear Algebra Appl. 322 (2001), 207–217.Google Scholar
Liu, X. and Yang, H., ‘Further results on the group inverses and Drazin inverses of anti-triangular block matrices’, Appl. Math. Comput. 218 (2012), 8978–8986.Google Scholar
Yang, H. and Liu, X., ‘The Drazin inverse of the sum of two matrices and its applications’, J. Comput. Appl. Math. 235 (2011), 1412–1417.Google Scholar
Zhou, J., Bu, C. and Wei, Y., ‘Group inverse for block matrices and some related sign analysis’, Linear Multilinear Algebra 60 (2012), 669–681.Google Scholar
Zhuang, W., The Guidance of Matrices over Skew Fields (Science Press, Beijing, 2006) (in Chinese).Google Scholar