Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T14:35:03.332Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Gauss-Green theorem

Published online by Cambridge University Press:  09 April 2009

B. D. Craven
B. D. Craven
Affiliation:
University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper [1], Green's theorem for line integrals in the plane was proved, for Riemann integration, assuming the integrability of Qx−Py, where P(x, y) and Q(x, y) are the functions involved, but not the integrability of the individual partial derivatives Qx and Py. In the present paper, this result is extended to a proof of the Gauss-Green theorem for p-space (p ≥ 2), for Lebesgue integration, under analogous hypotheses. The theorem is proved in the form 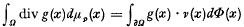where Ω is a bounded open set in Rp (p-space), with boundary Ω; g(x) =(g(x1)…, g(xp)) is a p-vector valued function of x = (x1,…,xp), continuous in the closure of Ω; 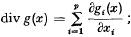μv,(x) is p-dimensional Lebesgue measure; v(x) = (v1(x),…, vp(x)) and Φ(x) are suitably defined unit exterior normal and surface area on the ‘surface’ ∂Ω and g(x) · v(x) denotes inner product of p-vectors.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 385 - 396
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Craven, B. D., ‘A note on Green's theorem’, J. Austral. Math. Soc. 4 (1964), 289–292.Google Scholar
[2]Potts, D. H., ‘A note on Green's theorem’, J. Lond. Math. Soc. 26 (1951), 302–304.Google Scholar
[3]Federer, W., ‘The Gauss-Green theorem’, Trans. Amer. Math. Soc. 58 (1945), 44–76.Google Scholar
[4]Federer, W., ‘Coincidence functions and their integrals’, Trans. Amer. Math. Soc. 59 (1946), 441–466.Google Scholar
[5]Federer, W., ‘Measure and area,’ Bull. Amer. Math. Soc. 58 (1952), 306–378.Google Scholar
[6]Michael, J. H., ‘Integration over parametric surfaces’, Proc. Lond. Math. Soc., Third Ser. 7 (1957), 616–640.Google Scholar
[7]Carathéodory, C., Vorlesungen über Reelle Funktionen (Teubner, 1927).Google Scholar
[8]Michael, J. H., ‘An n-dimensional analogue of Cauchy's integral theorem’, J. Austral. Math. Soc. 1 (1960), 171–202.CrossRefGoogle Scholar
[9]Saks, S., Theory of the integral (Second edition).Google Scholar