Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T14:02:07.540Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE BITS COUNTING FUNCTION OF REAL NUMBERS

Part of: Discrete mathematics in relation to computer science Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  01 August 2008

TANGUY RIVOAL
TANGUY RIVOAL*
Affiliation:
Institut Fourier, CNRS UMR 5582/Université Grenoble 1, 100 rue des Maths, BP 74, 38402 Saint-Martin d’Hères cedex, France (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Bn(x) denote the number of 1’s occurring in the binary expansion of an irrational number x>0. A difficult problem is to provide nontrivial lower bounds for Bn(x) for interesting numbers such as 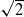, e or π: their conjectural simple normality in base 2 is equivalent to Bn(x)∼n/2. In this article, amongst other things, we prove inequalities relating Bn(x+y), Bn(xy) and Bn(1/x) to Bn(x) and Bn(y) for any irrational numbers x,y>0, which we prove to be sharp up to a multiplicative constant. As a by-product, we provide an answer to a question raised by Bailey et al. (D. H. Bailey, J. M. Borwein, R. E. Crandall and C. Pomerance, ‘On the binary expansions of algebraic numbers’, J. Théor. Nombres Bordeaux16(3) (2004), 487–518) concerning the binary digits of the square of a series related to the Fibonacci sequence. We also obtain a slight refinement of the main theorem of the same article, which provides a nontrivial lower bound for Bn(α) for any real irrational algebraic number. We conclude the article with effective or conjectural lower bounds for Bn(x) when x is a transcendental number.

Keywords

binary expansionsalgebraic numbers

MSC classification

Secondary: 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc. 68R01: General
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 1 , August 2008 , pp. 95 - 111
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Adamczewski, B. and Bugeaud, Y., ‘On the complexity of algebraic numbers I. Expansions in integer bases’, Ann. Math. 165(2) (2007), 547–565.CrossRefGoogle Scholar
[2]Adamczewski, B., Bugeaud, Y. and Luca, F., ‘Sur la complexité des nombres algébriques’, C. R. Acad. Sci. Paris 339 (2004), 11–14.CrossRefGoogle Scholar
[3]Allouche, J.-P. and Shallit, J., Automatic Sequences. Theory, Applications, Generalizations (Cambridge University Press, Cambridge, 2003).Google Scholar
[4]Bailey, D. H. and Borwein, J. M., Mathematics by Experiments: Plausible Reasoning in the 21st Century (A. K. Peters, Natick, MA, 2004).Google Scholar
[5]Bailey, D. H., Borwein, J. M., Crandall, R. E. and Pomerance, C., ‘On the binary expansions of algebraic numbers’, J. Théor. Nombres Bordeaux 16(3) (2004), 487–518.Google Scholar
[6]Blanchard, A. and Mendès-France, M., ‘Symétrie et transcendance’, Bull. Sci. Math. (2) 106(3) (1982), 325–335.Google Scholar
[7]Bundschuh, P., ‘Irrationalitätsmaße für e a, rational oder Liouville-Zahl’, Math. Ann. 192 (1971), 229–242.CrossRefGoogle Scholar
[8]Davis, C. S., ‘Rational approximations to e’, J. Aust. Math. Soc. 25 (1978), 497–502.CrossRefGoogle Scholar
[9]Duffin, R. J. and Schaeffer, A. C., ‘Khintchine’s problem in metric diophantine approximation’, Duke Math. J. 41 (1941), 241–255.Google Scholar
[10]Harman, G., Metric Number Theory, London Mathematical Society Monographs, 18 (Clarendon Press/Oxford University Press, New York, 1998).CrossRefGoogle Scholar
[11]Hata, M., ‘Rational approximations to π and some other numbers’, Acta Arith. 63(3) (1993), 335–349.CrossRefGoogle Scholar
[12]Kempner, A. J., ‘On transcendental numbers’, Trans. Amer. Math. Soc. 17 (1916), 476–482.Google Scholar
[13]Knight, M. J., ‘An ‘ocean of zeroes’ proof that a certain non-Liouville number is transcendental’, Amer. Math. Monthly 98 (1991), 947–949.Google Scholar
[14]Lehr, S., Shallit, J. and Tromp, J., ‘On the vector space of the automatic reals’, Theoret. Comput. Sci. 163(1–2) (1996), 193–210.Google Scholar
[15]Lindström, B., ‘On the binary digits of a power’, J. Number Theory 65(2) (1997), 321–324.CrossRefGoogle Scholar
[16]Niven, I., Irrational Numbers, The Carus Mathematical Monographs, 11 (1967).Google Scholar
[17]Nishioka, K., Mahler Functions and Transcendence, Lecture Notes in Mathematics, 1631 (Springer, Berlin, 1996).CrossRefGoogle Scholar
[18]Ridout, D., ‘Rational approximations to algebraic numbers’, Mathematika 4 (1957), 125–131.CrossRefGoogle Scholar
[19]Rivoal, T., ‘Convergents and irrationality measures of logarithms’, Rev. Mat. Iberoamericana 23(3) (2007), 931–952.Google Scholar
[20]Roth, K. F., ‘Rational approximations to algebraic numbers’, Mathematika 2 (1955), 1–20 (Corrigendum 168)CrossRefGoogle Scholar
[21]Stolarsky, K. B., ‘The binary digits of a power’, Proc. Amer. Math. Soc. 71(1) (1978), 1–5.CrossRefGoogle Scholar
[22]Zeckendorf, E., ‘Représentation des nombres naturels par une somme des nombres de Fibonacci ou de nombres de Lucas’, Bull. Soc. Roy. Sci. Liège 41 (1972), 179–182.Google Scholar