Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T14:27:53.727Z Has data issue: false hasContentIssue false
  • English
  • Français

On the behaviour of the characteristic function of a probability distribution in the neighbourhood of the origin

Published online by Cambridge University Press:  09 April 2009

E. J. G. Pitman
E. J. G. Pitman
Affiliation:
The Johns Hopkins UniversityBaltimore, Md. and The University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

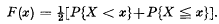Let X be a real valued random variable with probability measure P and distribution function F. It will be convenient to take F as the intermediate distribution function defined by . In mathematical analysis it is a little more convenient to use this function rather than 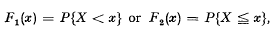, which arise more naturally in probability theory. In all cases we shall consider 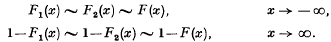With this definition, if the distribution function of X is F(x), then the distribution function of −X is 1−F(−x). The distribution of X is symmetrical about 0 if F(x) = 1 − F(−x).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 423 - 443
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Pitman, E. J. G., ‘Some theorems on characteristic functions of probability distributions’. Proc. Fourth Berkeley Symp. Math. Statist. Prob. (1960) 2, 393–402Google Scholar
[2]Karamata, M. J., ‘Sur un mode de croissance régulière des fonctions’. Mathematica (Cluj), V. iv, (1930) 38–53.Google Scholar
[3]Karamata, M. J., ‘Sur un mode de croissance régulière.Théorèmes fondamentaux’. Bull. de la soc. math. de France. 61 (1933) 55–62.Google Scholar
[4]Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis (Cambridge University Press, 4th ed. 1927).Google Scholar
[5]Durell, C. V. and Robson, A., Advanced Trigonometry (G. Bell and Sons, 1930).Google Scholar